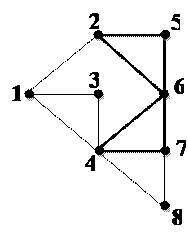Приложение 3. Расчет плотности графа.

 

Алгоритм нахождения плотности графа:

В качестве примера рассмотрим граф, изображенный на рис. П1.

 

1. Сопоставляем корню дерева заданный граф.

 

2. Фиксируем в графе вершину с максимальной степенью, сопоставив её концу исходящей из корня дуги.

Степень вершины v6 максимальна.

 

3. Строим множество исходящих из корня дуг. Их число – мощность носителя неокрестности вершины с максимальной степенью.

 

4. Считаем концы построенного яруса корнями новых деревьев. Устанавливаем, помечена ли вершина V символом пустое множество. Если нет, строим следующий ярус. Если да – конец алгоритма.

 

5. Пути между концами дуг, исходящих из корня синтезированного дерева, и висячими вершинами определяют полные подграфы заданного графа.

 

Рассмотрим применение этого алгоритма для приведенного графа.

 

 

а) б)

Рис. П1. Исходный граф (а) и построенное дерево (б). Получившиеся подграфы {4,6,7}, {4,7,8}, {1,3,4}

 

Построим ещё одно дерево для вершины v6, чтобы проверить, все ли полныеподграфы мы нашли. Все действия аналогичны. Рис. П2.

 

 

 

Рис. П2. Получили ещё два полных подграфа {2,5,6} и {4,6,7}, который уже был получен..

 

Таким образом, получили 4 полных подграфа с наибольшей степенью 3. Следовательно плотность графа равна трем.

 

Литература

1. Колесников А.В. Дискретная математика. Задания и методические указания к курсовой работе для студентов специальности 080801.65 «Прикладная информатика в экономике» (очно-заочная форма обучения). Калининград, 2006, 45 стр.

2. Кузнецов О.М., Адельсон-Вельский Г.М. Дискретная математика для инженера. - М.: Энергоатомиздат, 1988, 480 с.

3. Пономарев. В.Ф. Основы дискретной математики: Учебное пособие. – Калининград: КГТУ, 1997, 165 с.

4. Пономарев В.Ф. Дискретная математика для информатиков-экономистов. Учебное пособие. – Калининград: КГТУ и КИМБ, 2002, 239с.

5. Непейвода Н. Н. Прикладная логика: Учеб. Пособие.- 2-е изд., испр. и доп.- Новосибирск, изд-во Новосиб. Ун-та, 2000.-521с.

6. Горбатов В.А. Фундаментальные основы дискретной математики. М, Наука, ФМ, 200, 540 стр.