Их применения при движении одиночных газовых пузырьков
В 70-е годы на кафедре разработки и эксплуатации нефтяных месторождений МИНХ и ГП им. И.М. Губкина был выполнен большой цикл экспериментальных исследований по данной проблеме с целью оценки влияния на относительную скорость движения газовых пузырьков расходов жидкости и газа, условий стесненного движения газовых пузырьков, поверхностного натяжения и конфигурации вертикальных каналов (круглая труба, кольцо, серповидный канал). Кроме того, изучалось влияние указанных параметров на относительную скорость движения газовых пузырьков на режиме нулевой подачи жидкой фазы (движение газовых пузырьков в неподвижной жидкости), что является практически важным для исследования работы не только затрубного пространства добывающих скважин, но также и работы газлифтных подъемников в процессе их пуска в работу. Решались и другие задачи, связанные с образованием газовых пузырьков в различных диспергирующих устройствах, а также изучалось влияние угла наклона подъемника на относительную скорость газовой фазы. В качестве жидкой фазы использовалась вода с добавками различных количеств изопропилового спирта, что позволило изменять поверхностное натяжение в системе «раствор изопропилового спирта — воздух» от 72 до 45 мН/м. Исследования проведены на экспериментальной установке, принципиально не отличающейся от подобных установок. Обработка фотографий газожидкостных смесей позволила построить кривые распределения количества газовых пузырьков по диаметру, которые подчиняются нормальному закону распределения. При этом диаметры газовых пузырьков изменялись от 0,1 до 0,6 мм. Средний диаметр, соответствующий максимуму кривой распределения, составил 0,34 мм. Эти размеры газовых пузырьков достаточно хорошо согласуются с таковыми в добывающих скважинах, что свидетельствует о возможности практического использования полученных результатов. Экспериментальные исследования проводились в два этапа: на первом этапе изучалось движение газовых пузырьков в неподвижной жидкости (режим нулевой подачи), а на втором — в движущейся жидкости. Остановимся вкратце на полученных результатах. 2.1.3. Плотность газожидкостной смеси Основное определение плотности любой однородной среды может быть применено к газожидкостной смеси с учетом следующего. Так как газожидкостная смесь является неоднородной средой, состоящей из жидкой и газовой фаз различных объемов, то для определения плотности такой неоднородной среды объем ее должен выбираться в соответствии с неоднородностью. Во избежание больших ошибок в определении плотности газожидкостной смеси необходимо брать объемы, в сотни раз превышающие объемы частиц дисперсной фазы. Плотность газожидкостной смеси ρсм определим так:
где V ж, V г— объемы жидкости и газа соответственно, м3; V го— объем газа V гпри нормальных условиях, м3; ρго — плотность газа при нормальных условиях, кг/м3. При этом должно соблюдаться следующее условие (когда газ является дисперсной фазой):
При известных объемных расходах жидкой и газовой фаз средняя плотность газожидкостной смеси определяется аналогично уравнению (2.19):
где q, V — объемные расходы жидкой и газовой фаз соответственно, м3/с. Уравнение (2.21) справедливо для случая, когда относительная скорость движения газа υ оравна 0. 2.1.4. Плотность смеси «жидкость (нефть)—газ» Рассмотрим случай восходящего движения газожидкостной смеси в круглой вертикальной трубе площадью сечения f при существовании относительной скорости. Наличие относительной скорости приведет к тому, что при одинаковых объемных расходах жидкой q и газовой V фаз площади, занимаемые каждой фазой в сечении трубы, будут различны. При этом площадь, занимаемая газовой фазой, будет все время уменьшаться при увеличении относительной скорости. В общем виде плотность газожидкостной смеси можно записать в виде функциональной зависимости:
Так как площадь поперечного сечения лифта при движении газожидкостной смеси занята жидкой фазой f ж и газовой фазой f г, то можно записать следующие очевидные равенства:
где υ ж, υ г — истинные скорости жидкой и газовой фаз, м/с. В равенствах (2.23-2.25) параметры υ ж, υ г, f ж и f г практически очень трудно определить. Найдем функциональную связь между основными параметрами газожидкостной смеси, которые сравнительно легко могут быть определены. Рассмотрим объем газожидкостной смеси в вертикальной трубе высотой Δ h, плотность смеси в которой определяется уравнением (2.19) с соблюдением условия (2.20). Для данного элементарного объема выражения V ж, V гмогут быть записаны так:
С учетом уравнений (2.26), (2.27) и (2.28) уравнение (2.19) может быть переписано в виде:
С учетом выражения (2.25) можно переписать (2.29) в виде:
Перепишем выражение (2.9) с учетом (2.23, 2.24 и 2.25):
или с учетом (2.30):
После решения (2.32) относительно ρсм получаем:
Учитывая истинное газосодержание φ, определяемое по (2.6), выражение (2.29) с учетом (2.25) можно переписать в таком виде:
С учетом (2.2) и (2.7) выражение (2.33) перепишем так:
где β — объемное расходное газосодержание.
и назовем его параметром относительной скорости. Найдем взаимосвязь между объемным расходным и истинным газосодержанием. Запишем (2.31) в виде:
или
После несложных преобразований (2.37) и решения квадратного уравнения относительно φ, получим:
или
Для нисходящего вертикального потока газожидкостной смеси взаимосвязь основных характеристик такова:
Анализ данного выражения показывает, что оно может существовать только при выполнении следующего условия:
— в восходящем потоке ГЖС при постоянном объемном расходном газосодержании β истинное газосодержание φ снижается по мере роста параметра R (при росте относительной скорости и снижении приведенной скорости жидкости q/f); — в нисходящем потоке ГЖС каждому фиксированному значению параметра R соответствует свое собственное и единственное значение минимального истинного газосодержания φмин, а само истинное газосодержание φ больше объемного расходного β. Для нисходящего течения на рис. 2.1 нанесены экспериментальные точки притечении ГЖС в нисходящем наклонном трубопроводе для чисел Фруда по смеси Frсм = 4. Легко показать, что между параметрами
существует следующая взаимосвязь:
Таким образом, хорошее качественное совпадение теоретических зависимостей φ = f (β, R) с экспериментальными данными говорит о правильности физики рассматриваемого явления. Для упрощения расчетов по (2.33) и (2.35) в отдельных случаях можно пренебречь массой газа (ρг = 0). Тогда зависимость (2.33) примет вид:
а зависимость (2.35) запишется так:
На рис. 2.2. представлена зависимость относительной плотности смеси ρсм/ρж от относительной скорости газовой фазы υ0 при постоянных величинах V, q и f, построенная по выражению (2.44), откуда видно, что по мере роста относительной скорости υ0 увеличивается и относительная плотность смеси, т.е. относительная скорость является существенным параметром, с помощью которого можно управлять плотностью ГЖС. При относительной скорости газовой фазы, равной υ0 = 0, плотность ГЖС минимальна и будем называть ее «идеальной» плотностью смеси
|


 К настоящему времени наиболее изученными являются вопросы движения ГЖС в вертикальных каналах круглого сечения при эмульсионной структуре потока. Движение же газовых пузырьков в стесненных условиях при значительном изменении физических свойств фаз не только в каналах кольцевого сечения, но также и в каналах круглого сечения остаются изученными недостаточно, хотя в практике эксплуатации добывающих скважин движение ГЖС осуществляется и в каналах кольцевого сечения. Кроме того, практически неизученными остаются и вопросы движения ГЖС в наклонных каналах различных форм сечения.
К настоящему времени наиболее изученными являются вопросы движения ГЖС в вертикальных каналах круглого сечения при эмульсионной структуре потока. Движение же газовых пузырьков в стесненных условиях при значительном изменении физических свойств фаз не только в каналах кольцевого сечения, но также и в каналах круглого сечения остаются изученными недостаточно, хотя в практике эксплуатации добывающих скважин движение ГЖС осуществляется и в каналах кольцевого сечения. Кроме того, практически неизученными остаются и вопросы движения ГЖС в наклонных каналах различных форм сечения.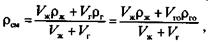 (2.19)
(2.19) (2.20)
(2.20) (2.21)
(2.21)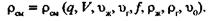 (2.22)
(2.22) (2.23)
(2.23)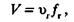 (2.24)
(2.24)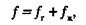 (2.25)
(2.25) (2.26)
(2.26)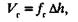 (2.27)
(2.27)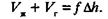 (2.28)
(2.28)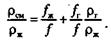 (2.29)
(2.29)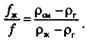 (2.30)
(2.30) (2.31)
(2.31)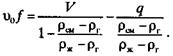 (2.32)
(2.32) (2.33)
(2.33)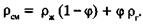 (2.34)
(2.34)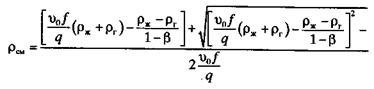 (2.35)
(2.35)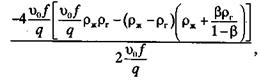
 Обозначим через R комплекс
Обозначим через R комплекс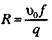 (2.36)
(2.36)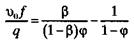
 (2.37)
(2.37)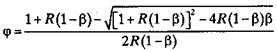 (2.38)
(2.38)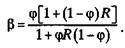 (2.39)
(2.39)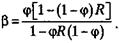 (2.40)
(2.40)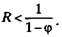 (2.41)
(2.41)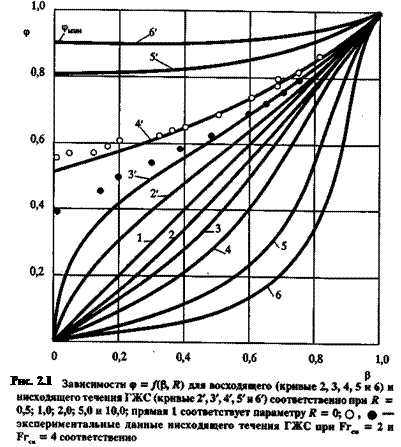 Совместное рассмотрение (2.40) и (2.41) позволяет сделать принципиальный вывод о том, что в случае нисходящего движения ГЖС, когда соблюдается условие (2.10) зависимость (2.40) существует при любых значениях β и φ от 0 до 1 только при параметре относительной скорости < 1. При R > 1 существует некоторое минимальное значение φмин, ниже которого невозможно само существование газожидкостной смеси. На рис. 2.1представлены графические зависимости φ = f (β, R), анализ которых показывает:
Совместное рассмотрение (2.40) и (2.41) позволяет сделать принципиальный вывод о том, что в случае нисходящего движения ГЖС, когда соблюдается условие (2.10) зависимость (2.40) существует при любых значениях β и φ от 0 до 1 только при параметре относительной скорости < 1. При R > 1 существует некоторое минимальное значение φмин, ниже которого невозможно само существование газожидкостной смеси. На рис. 2.1представлены графические зависимости φ = f (β, R), анализ которых показывает: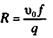 и (
и (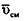 — приведенная скорость движения газожидкостной смеси)
— приведенная скорость движения газожидкостной смеси)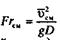
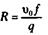
 (2.42)
(2.42) ((2.43)
((2.43)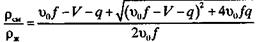 (2.44)
(2.44)
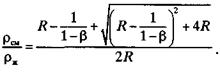 (2.45)
(2.45)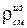 .
.


