Вычисление координат вершин теодолитного хода выполняют в специальной ведомости (прил. 3)
Стоимость струганных бревен, за метраж или кубатуру в зависимости от диаметра. моя почта kness2009@yandex.ru; тел: 8-902-11-00-727 Обработка журнала измерения горизонтальных углов (прил. 2) Необходимо обработать журнал в соответствии с примером, приведенным на станции 1 теодолитного хода. В столбце 5 на станциях 2,3,4 требуется вычислить значения углов в полуприеме, как разницу из отсчетов по горизонтальному кругу, полученных при КЛ и КП (значения отсчетов выбирают по варианту из прил.2а). В столбце 6 из вычисленных углов в полуприеме определить среднее значение. В столбце 8 необходимо определить средние значения длин линий теодолитного хода (с точностью до см). Вычисление координат вершин теодолитного хода выполняют в специальной ведомости (прил. 3) 2.1 Определение угловой невязки теодолитного хода. Необходимо из журнала измерений горизонтальных углов (прил. 2) перенести в ведомость вычисления координат (столбец 2 прил. 3) вычисленные средние значения углов и определить их практическую сумму - Σβпр, которую записывают внизу столбца 2. Под ней выписывают теоретическую сумму углов (как сумму углов многоугольника) Σβтеор , полученную по формуле:
где n – количество углов теодолитного хода. Угловую невязку
Полученную угловую невязку
где Т – точность теодолита. Если угловая невязка меньше допустимой 2.2. Уравнивание углов теодолитного хода. Угловую невязку распределяют с обратным знаком равномерно на все измеренные углы в виде поправок С учетом поправок находят исправленные (уравненные) углы и записывают в столбец 3:
где
Алгебраическая сумма исправленных углов должна быть равна теоретической сумме углов многоугольника, т.е. 2.3 Вычисление дирекционных углов линий теодолитного хода Дирекционные углы линий α (столбец 4) вычисляют по формуле:
где
Пример Дирекционный угол стороны теодолитного хода
Контролем вычислений будет получение исходного дирекционного угла В столбце 5 полученные по формуле (5) дирекционные углы переводят в румбы. 2.4 Вычисление горизонтальных проложений линий теодолитного хода Используя данные прил. 2, вычисляют горизонтальные проложения
где
Пример Горизонтальное проложение линии 1-2 равно:
Следует обратить внимание на углы наклона линий (см. прил. 2) и, если он менее 1°30′, то поправку за наклон линии не вводят, тогда горизонтальное проложение приравнивают к измеренной длине линии Горизонтальные проложения записывают в столбец 6. 2.5 Вычисление приращений координат по осям X и Y Приращения координат
где
Приращения координат вычисляют до сотых долей метра (столбцы 7, 8). Пример Приращения координат линии 1-2 равны:
Вычисляют практическую сумму полученных приращений координат 2.6 Вычисление линейных невязок по осям координат Невязки по осям координат определяют, как разность практических сумм вычисленных приращений координат и теоретических сумм приращений координат, которые определяют по формулам:
где
Т.к. теодолитный ход замкнутый, то Таким образом, для замкнутого теодолитного хода линейные невязки
где 2.7. Вычисление абсолютной и относительной невязок приращений координат Абсолютную невязку
где Относительную невязку вычисляют по формуле:
где
Относительная невязка должна быть не более 1/2000, т.е. При выполнении данного условия приступают к уравниванию приращений координат. 2.8. Уравнивание приращений координат Для уравнивания полученные линейные невязки
где
Поправки записывают в целых сантиметрах над вычисленными приращениями координат со своим знаком. Пример Поправки в приращения координат линии 1-2 равны:
Вычисление поправок контролируют равенствами: Исправленные приращения координат вычисляют с учетом поправок и записывают в ведомость (столбцы 9, 10) по формулам:
где
Алгебраическая сумма исправленных приращений координат должна быть равна теоретической сумме приращений координат, т.е. 2.9. Вычисление координат вершин теодолитного хода Из прямой геодезической задачи координаты вершин полигона вычисляют последовательным прибавлением (со своим знаком) исправленных приращений координат к координатам предыдущей вершины (столбцы 11, 12):
где
Пример Координаты второй вершины теодолитного хода равны:
Контролем вычислений будет получение исходных координат первой вершины теодолитного хода Построение и оформление плана теодолитной съемки Построение плана снятого участка местности необходимо выполнить в масштабе 1:500 на ватмане формата А-3 в следующей последовательности: · построение координатной сетки (сетки квадратов) со сторонами 100×100 мм; · нанесение вершин теодолитного хода по вычисленным координатам на план; · построение контурного плана участка местности по материалам теодолитной съемки. 3.1. Построение координатной сетки Сетку координат строят на листе ватмана формата А-3. Сторона квадрата сетки принимается для масштаба 1:500 равной 100 мм (что составляет 50 м на местности). Для получения правильного прямоугольника выполняют следующие построения с помощью измерителя и точной металлической линейки: · через углы листа ватмана проводят диагонали и от их пересечения откладывают равные отрезки, полученные точки соединяют горизонтальными и вертикальными линиями; · диагонали убирают резинкой и на полученных сторонах прямоугольника откладывают отрезки по 100 мм, т.о. получают координатную сетку в виде квадратов. Сетку проверяют по сторонам и диагоналям каждого квадрата в отдельности, отклонения построенных размеров от заданных не должно превышать 0,2 мм; · сетку координат оцифровывают так, чтобы все вершины теодолитного хода располагались внутри рамки симметрично, для этого перед разбивкой сетки из ведомости вычисления координат (прил. 3) выбирают максимальные и минимальные координаты по оси абсцисс и по оси ординат и, согласно им, разбивают и подписывают сетку числами, кратными 50 метрам. · изображение сетки следует выполнять тонкими линиями так, чтобы внутренние линии в последствии легко стирались; пересечение этих линий фиксируют сохраняемыми крестиками со сторонами 6 мм и оформляют на плане зеленой тушью.
3.1. Нанесение вершин теодолитного хода по вычисленным координатам на план Вершины теодолитного хода наносят на план по их вычисленным координатам (см. прил. 3) в масштабе 1:500. Пример
Полученную точку обозначают слабым наколом иглы циркуля-измерителя и обводят окружность диаметром 1,5 мм; внутри этой окружности никакие линии проводить нельзя. Слева записывают номер точки. Нанесение на план вершин теодолитного хода необходимо проконтролировать. Для контроля измеряют расстояния между нанесенными вершинами: получившиеся на плане длины сторон должны быть равны вычисленным горизонтальным проложениям в ведомости координат (см. прил. 3). Пример Горизонтальное проложение стороны 1-2 теодолитного хода равно 89,99 м, следовательно, в масштабе плана расстояние между нанесенными вершинами должно быть 18,0 см. Допустимое расхождение – 0,2 мм в плане. 3.1. Построение контурного плана участка местности по материалам теодолитной съемки В приложении 4 приведены абрисы теодолитной съемки сторон и точек съемочного обоснования. На абрисах все измеренные расстояния приведены в м. Для составления плана необходимо, используя данные абриса, откладывать соответствующие расстояния или углы от сторон теодолитного хода методами перпендикуляров, полярных координат, угловых и линейных засечек, створов. Способ перпендикуляров Если при съемке применялся способ перпендикуляров, это означает, что измерялось расстояние по стороне теодолитного хода от станции съемочного обоснования до основания перпендикуляра и длина перпендикуляра до снимаемой точки (см. рис. 3.а). Следовательно, для того, чтобы нанести данную точку на план, необходимо с помощью линейки отложить измеренное расстояние от точки съемочного обоснования, восстановить перпендикуляр и отложить его длину, при этом все измеренные расстояние переводят в масштаб плана, например, 23,57 м на местности соответствуют 4,7 см в плане данного масштаба (см. рис. 3б).
Способ полярных координат С точки теодолитного хода, принимаемой за полюс, положение каждой характерной точки местности определяют с помощью полярных координат, к которым относятся: угол между линией теодолитного хода и направлением на снимаемую точку, а также расстояние до нее. На местности с помощью теодолита от ориентирной линии измеряют полярные углы bi, расстояние Si – рулеткой (см. рис. 4.а). На план точки наносят с помощью транспортира и линейки. Центр транспортира совмещают с полюсом (точкой теодолитного хода), нулевой отсчет устанавливают по ориентирному направлению (стороне теодолитного хода), и от него по ходу часовой стрелки отмечают величины углов. По полученным направлениям в масштабе плана откладывают расстояния, получают снимаемые точки (см. рис. 4.б).
Способ угловой засечки
Способ линейной засечки
Способ створов
После нанесения всех точек ситуации все дополнительные построения (перпендикуляры, дуги и т.п.) вытирают резинкой, оставляя только объекты местности. Оформление плана участка местности Все контура, изображаемые на плане, вычерчиваются тушью в соответствии с условными знаками (прил.5) или [4]. При этом необходимо тщательно выдерживать очертания и размеры, а также порядок, приведенные в [4] для масштаба 1:500. Все построения и надписи выполняют тонкими линиями. Координаты линий сетки указываются только в углах плана. Точки пересечения линий сетки координат фиксируются крестиками зеленым цветом. Вверху плана за пределами координатной сетки плана наносят надпись – «План участка местности». Внизу, посередине, указывают масштаб, ниже – «В одном сантиметре 5 метров». Еще ниже – «Сплошные горизонтали проведены через 0.5 метра». В правом нижнем углу должна быть надпись – «Составил студ. гр……Иванов И.И.». Образец оформление плана приведен в прил. 6. ЛИТЕРАТУРА 1. Кулешов Д.А., Стрельников Г.Е. Инженерная геодезия для строителей. – М.: Недра, 1990. 2. Куштин И.Ф., Куштин В.И. Инженерная геодезия. – Ростов – на – Дону: Феникс,2002. 3. Маслов А.В. Геодезия. – М.: Недра, 1980. 4. Условные знаки для топографических планов масштабов 1:5000 ÷ 1:500. – М.: Недра, 1989.
Приложение 1
Схема планового съемочного обоснования
Составил: студ. гр.__________________________
Приложение 2
Журнал измерения горизонтальных углов
Наблюдал:____________________________
Приложение 2а ВАРИАНТЫ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ
Продолжение прил. 2а ВАРИАНТЫ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ
Продолжение прил. 2а ВАРИАНТЫ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ
|
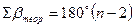, (1)
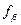вычисляют по формуле:
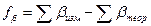. (2)
:
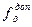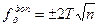, (3)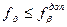
, то приступают к уравниванию углов.
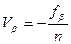, которые выписывают над секундами измеренных углов в столбце 2. Вычисление поправок контролируют равенством 
.
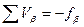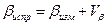, (4)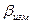
– измеренные углы теодолитного хода;
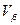– поправки в углы.
.
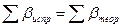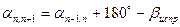, (5)
– дирекционный угол последующей линии теодолитного хода;
– дирекционный угол предыдущей линии теодолитного хода;
– исправленный угол теодолитного хода.
равен:
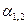начальной линии 1-2.
сторон теодолитного хода по формуле: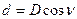
, (6)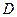
– длина линии теодолитного хода, измеренная с помощью ленты (среднее значение из измеренных в прямом и обратном направлениях);
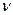– угол наклона данной лини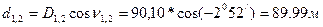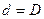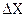и.
.
.
и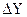 
определяют путем решения прямой геодезической задачи по формулам:
, 
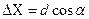, (7)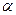
– дирекционный угол этой линии.
;
.
, 
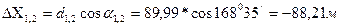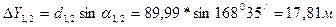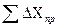и записывают внизу столбцов 7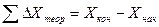, 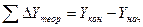8.
, 
, (8)
, 
– координаты конечной точки теодолитного хода;
, 
, 
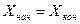, следовательно, теоретические суммы приращений координат равны нулю.
и 
по осям координат определяют по формулам: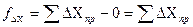
, 
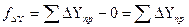, (9)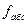
определяют по формуле:
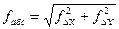, (10)
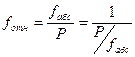, (11)
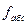– абсолютная невязка;
– периметр теодолитного хода.
.
, 
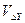по формулам:
, 
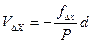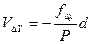, (12)
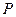– периметр теодолитного хода.
;
.
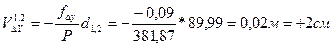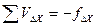и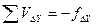 
.
, 
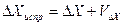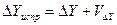, (13)
, 
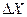– вычисленные приращения координат;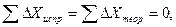
.
, 
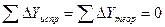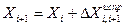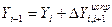, (14)
, 
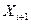– координаты последующей вершины теодолитного хода;
, 
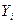– координаты предыдущей вершины теодолитного хода;
, 
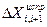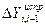– исправленные приращения координат данной линии теодолитного хода.
;
.
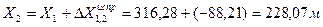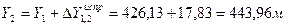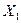и 
.
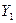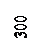
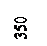
Необходимо нанести на план точку 1 с координатам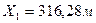и 
и 
. Сначала выясняют, в каком из квадратов должна лежать эта точка: по направлению X точка должна находится между линиями сетки с абсциссами 300 и 350 м, по направлению Y - между линиями сетки с ординатами 400 и 450 м (рис. 2). От линии с абсциссой 300 по вертикальным сторонам этого квадрата вверх откладывают расстояние 316,28-300 =16,28 м переведенное в масштаб плана (3,25 см) и проводят линию, параллельную линии с абсциссой 300 м. Вдоль нее от вертикальной линии сетки с ординатой 400 м откладывают вправо расстояние 426,13-400=26,13 м переведенное в масштаб плана (5,2 см).
В способе угловой засечки по стороне теодолитного хода рулеткой измеряется произвольное расстояние, например 75 м (см. рис. 5.а). В полученных точках измеряются углы между линией хода инаправлением на снимаемую точку местности. Построения на плане начинают с откладывания в масштабе измеренного расстояния (75 м соответствует 15 см). В полученных точках, с помощью транспортира, строят углы от твердой линии теодолитного хода. Положение искомой точки будет в месте пересечения двух направлений (см. рис. 5.б).
В способе линейной засечки рулеткой измеряются расстояние по стороне теодолитного хода (30 м), а также расстояния до снимаемой точки (см. рис. 6.а). Нанесение на плане точки, снятой данным способом, заключается в построении треугольника по трем известным сторонам, из которых одна является базисом (30 м – в масштабе плана 6 см), две других берутся циркулем, и в пересечении дуг, описанных из концов базиса, получается положение снятой точки (см. рис. 5.б).
Способ применяется, когда сторону (створ) теодолитного хода пересекает линейное сооружение или контур местности. В процессе съемки рулеткой измеряют расстояния по стороне теодолитного хода от станции до пересечения с объектом местности (см. рис. 6.а). При построениях, линейкой откладывают эти расстояния, переведенные в масштаб плана (см. рис. 6.б).
