Нахождение энергии электрона из модели БораВычислим уровни энергии атома водорода без учета тонкой структуры, используя простую модель атома Бора. Для этой цели можно сделать грубое допущение электрона, двигающегося по круговой орбите на фиксированном расстоянии. Происходит это под действием кулоновской силы, равной
Здесь me - масса электрона, vn - его скорость на орбите радиуса rn, ε0 - диэлектрическая проницаемость вакуума (электрическая постоянная). Отсюда кинетическая энергия электрона
где r - расстояние от электрона до ядра. Потенциальная его энергия
Полная энергия, соответственно, равна
Для нахождения радиуса rn стационарной орбиты с номером n рассмотрим систему уравнений, в которой второе есть математическое выражение первого постулата Бора
Отсюда получаем выражение для радиуса стационарной орбиты с номером n:
Радиус первой орбиты оказывается равным Подставляя это значение в выражение для энергии, получим, что
Отсюда мы можем найти частоту фотона, излучаемого атомом водорода за один переход из возбужденного состояния с главным квантовым числом n1 в состояние с неким фиксированным главным квантовым числомn2.
где
|
. Тогда, после сокращения на 1 / rn,
:
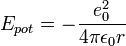
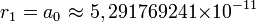метра. Эта константа называется боровским радиусом.
постоянная Ридберга (имеет размерность с− 1).
