Диагональный ход
Рис. 2.1 Дирекционные углы сторон и координаты точек, к которым примыкает диагональный ход, являются исходными для вычисления координат точек диагонального хода. Обработка диагонального хода производится в той же последовательности, что и основного хода. 2.2.1. Из журнала теодолитной съемки в ведомость вычисления координат выписывают: в графу 2 – измеренные горизонтальные углы; в графу 6 – горизонтальные проложения линий. 2.2.2. Из результатов обработки основного хода выбирают исходные дирекционные углы (a4-5 = 205°42,4'; a2-3 = 72°36,8'), которые записывают в графу 4 ведомости, и исходные координаты точек примыкания диагонального хода (Х5 = +494.77 м; У5 = +783.29 м; Х2 = +829.60 м; У2 = +562.04 м), которые переписывают в графы 11 и 12 ведомости. 2.2.3. Вычисляют сумму измеренных углов и теоретическую сумму углов. Теоретическая сумма углов в разомкнутом ходе вычисляется по формуле:
где aн и aк – исходные дирекционные углы. В примере åbизм. = 493°04,4'; aн = 205°42,4'; aк = 72°36,8';
2.2.4. Угловую невязку получают по формуле:
В нашем случае 2.2.5. Определяют допустимость угловой невязки по формуле:
В примере 2.2.6. Вычисляют поправки в измеренные углы и исправляют углы так же, как в основном ходе, и с такими же контрольными вычислениями. 2.2.7. Вычисляют дирекционные углы сторон хода. За исходный принимается a4-5. Вычисление дирекционных углов контролируется тем, что в конце вычислений должны получить дирекционный угол конечной стороны, равный заданному (a2-3). 2.2.8. Вычисляют румбы линий хода, приращения координат и невязки в приращениях координат. Невязки вычисляют по формулам:
где Теоретические суммы приращений координат вычисляются по формулам:
где хн, ун - координаты начальной точки диагонального хода (в примере х5, у5); хк, ук - координаты конечной точки диагонального хода (в примере х2, у2); В приведенном примере:
fx = + 0.13 м; fу = +0.25 м. Абсолютная невязка Относительная невязка диагонального хода должна удовлетворять условию: В примере 2.2.9. Распределение невязок и вычисление исправленных приращений координат производится так же, как в основном ходе, с соблюдением соответствующих контролей. Используя исходные координаты точек диагонального хода и исправленные приращения координат, вычисляют последовательно координаты вершин диагонального хода. 2.2.10. Контролируют вычисление координат следующим образом: в конце вычислений координат вершин диагонального хода должны получить исходные координаты конечной точки диагонального хода.
Составление плана теодолитной съемки.
|


 ,
,

 .
. .
. , т.е.
, т.е. 
 ,
,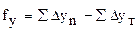 ,
, ,
,  – практические суммы приращений координат:
– практические суммы приращений координат:  ,
,  ,
, ,
, = – 334.96 м;
= – 334.96 м;  = – 221.00 м;
= – 221.00 м; = – 334.83 м;
= – 334.83 м;  = + 221.25 м;
= + 221.25 м; = 0.28 м.
= 0.28 м. £
£  .
. .
.


