Дифференцирующие цифровые фильтры.
Передаточная функция. Из выражения для производной d(exp(jwt))/dt = jw exp(jwt) следует, что при расчете фильтра производной массива данных необходимо аппроксимировать рядом Фурье передаточную функцию вида H(w) = jw. Поскольку коэффициенты такого фильтра будут обладать нечетной симметрией (h-n = -hn) и выполняется равенство hn [exp(jwn)-exp(-jwn)] = 2j hn sin nw, то передаточная характеристика фильтра имеет вид: H(w) = 2j(h1 sin w + h2 sin 2w +... + hN sin Nw), т.е. является мнимой нечетной, a сам фильтр является линейной комбинацией разностей симметрично расположенных относительно sk значений функции. Уравнение фильтрации: yn = Если дифференцированию подлежит низкочастотный сигнал, а высокие частоты в массиве данных представлены помехами, то для аппроксимации в пределах главного частотного диапазона задается (без индекса мнимости) передаточная функция фильтра вида: H(w) = w, w £ wв, H(w) = 0, wв< w £ wN. Оператор дифференцирующего фильтра: h(n) = (2/p) Принимая, как обычно, wN = p (Dt = 1) и решая (7.5.1) при H(w) = w, получаем: hn = (2/p)[sin(nwв)/n2 - wв cos(nwв)/n], (7.5.2) hо = 0, h-n = -hn. Частотная характеристика: Im(H(w)) = Точность дифференцирования. На рис. 7.5.1 приведен пример расчета коэффициентов дифференцирующего фильтра на интервал частот {0-0.5}p при Dt=1 (wв = p/2). Операторы дифференцирующих фильтров, как правило, затухают очень медленно и, соответственно, достаточно точная реализация функции (7.5.3) весьма затруднительна.
Ряд (7.5.3) усекается до N членов, и с помощью весовых функций производится нейтрализация явления Гиббса. Явление Гиббса для дифференцирующих фильтров имеет весьма существенное значение, и может приводить к большим погрешностям при обработке информации, если не произвести его нейтрализацию. Примеры ограничения оператора, приведенного на рис. 7.5.1, и соответствующие передаточные функции H'(w) усеченных операторов показаны на рис. 7.5.2. Для оценки возможных погрешностей дифференцирования усеченными операторами произведем расчет фильтра при wв = p/2. По формулам (7.5.2) определяем: h0-10 = 0, 0.3183, 0.25, -0.0354, -0.125, 0.0127, 0.0833, -0.0065, -0.0625, 0.0039, 0.05.
Произведем проверку работы фильтра на простом массиве данных sn = n, производная которого постоянна и равна 1. Для массива с постоянной производной фильтр может быть проверен в любой точке массива, в том числе и в точке n=0, для которой имеем: у = при этом получаем: у=0.5512 при N=5, у=1.53 при N=10.
Такое существенное расхождение с действительным значением производной объясняется тем, что при w=0 тангенс угла наклона реальных передаточных функций фильтра, как это видно на рисунке 7.5.2, весьма существенно отличается от тангенса угла наклона аппроксимируемой функции H(w) = w. На рис. 7.5.3 приведены частотные графики относительной погрешности дифференцирования s = Hн'(w)/Hн(w) с вычислением значений на нулевой частоте по пределам функций при N → ∞. На рис. 7.5.4 приведен пример операции дифференцирования гармоники s с частотой wo оператором с N=10 в сопоставлении с точным дифференцированием ds/dk.
Рис. 7.5.4. Пример операции дифференцирования. Применение весовых функций. Применим для нейтрализации явления Гиббса весовую функцию Хемминга. Результат нейтрализации для фильтра с N=10 приведен на рис. 7.5.5. Повторим проверочный расчет дифференцирования на массиве sn = n и получим результат у=1.041, т.е. погрешность дифференцирования уменьшается порядок.
Рис. 7.5.5. Дифференцирование с применением весовой функции. Аналогично производится расчет и полосовых дифференцирующих фильтров с соответствующим изменением пределов интегрирования в (7.5.1) от wн до wв. При этом получаем: hn = (wнcos nwн-wвcos nwв)/(np) + (sin nwв-sin nwн)/(n2p). Фильтры с линейной групповой задержкой. Дифференцирующие фильтры, а равно и любые другие фильтр с мнимой частотной характеристикой, например, оператор преобразования Гильберта, могут быть выполнены в каузальном варианте при условии обеспечения линейной групповой задержки сигнала, которое записывается следующим образом: j(w) = b - aw, (7.5.4) где b и a - константы. Оно выполняется, если импульсная характеристика фильтра имеет положительную симметрию: h(n) = -h(N-n-1), n = 0, 1, 2, …, (N-1)/2, N – нечетное (тип 1); n = 0, 1, 2, …, (N/2)-1, N – четное (тип 2). При этом фазовая характеристика будет определяться длиной фильтра: a = (N-1)/2, b = p/2. Частотная характеристика фильтра: H(w) = |H(w)| exp(jj(w)), (7.5.4) где модуль |H(w)| задается нечетным. Оба типа фильтров вводят в выходной сигнал сдвиг фазы на 90о. Кроме того, частотная характеристика фильтра типа 1 всегда равно нулю на частоте Найквиста, что определяется знакопеременностью левой и правой части главного диапазона спектра с учетом периодизации спектра дискретных функций. Курсовая работа 10-07. Разработать и исследовать оптимальный способ закругления частотной характеристики дифференциального фильтра и реализовать его в программе расчета фильтра и фильтрации цифровых данных..
|

 hn(sk+n - sk-n).
hn(sk+n - sk-n).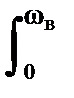 H(w) sin(npw/wN) dw, n = 0,1,2,... (7.5.1)
H(w) sin(npw/wN) dw, n = 0,1,2,... (7.5.1) hn sin nw = 2
hn sin nw = 2 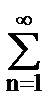 hn sin nw. (7.5.3)
hn sin nw. (7.5.3) Рис. 7.5.1. Коэффициенты оператора фильтра.
Рис. 7.5.1. Коэффициенты оператора фильтра.
 Рис. 7.5.2. Частотные функции фильтров.
Рис. 7.5.2. Частотные функции фильтров.
 hn so-n = 2
hn so-n = 2  n hn,
n hn, Рис. 7.5.3. Погрешность дифференцирования.
Рис. 7.5.3. Погрешность дифференцирования.





