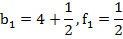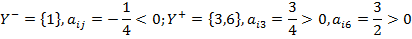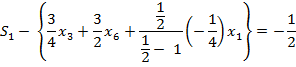Метод Гомори
Свойства «правильного отсечения (Гомори)»:
· линейные
· отсекает найденные оптимальные нецелочисленные решения задачи (1)-(3)
· не затрагивает ни одной из целочисленных точек задачи (1)-(4)
| Б
| 
|
| …
|
| …
|
| 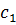
| …
| 
| …
| 
| В
|
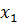
| …
| 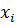
| …
| 
| 
| …
| 
| …
| 
|
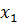
|
|
| …
|
| …
|
| 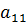
| …
| 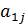
| …
| 
| 
|
| …
| …
| …
| …
| …
| …
| …
| …
| …
| …
| …
| …
| …
|
 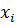
|
|
| …
|
| …
|
| 
| …
| 
| …
| 
| 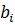
|
| …
| …
| …
| …
| …
| …
| …
| …
| …
| …
| …
| …
| …
|

|
|
| …
|
| …
|
| 
| …
| 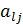
| …
| 
| 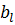
|
| …
| …
| …
| …
| …
| …
| …
| …
| …
| …
| …
| …
| …
|

|
|
| …
|
| …
|
| 
| …
| 
| …
| 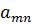
| 
|

|
| …
|
| …
|
| 
| …
| 
| …
| 
| F(x)
|
Найдено оптимальные, нецелочисленные решения ЗЛП (1) - (3)

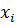 ∈ Б (базисные) переменные
∈ Б (базисные) переменные

 Б (небазисные)
Б (небазисные)
Пусть 
Ι. Полностью целочисленные задачи:
Выбор наиболее эффективного отсечения.
Пусть 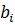 и
и 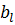 – нецелочисленные. Выбирают:
– нецелочисленные. Выбирают:
- строку, соответствующую 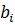 ∉ Z с наибольшей дробной частью:
∉ Z с наибольшей дробной частью:
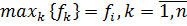

- если 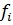 =
= 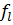 , выбирают строку, которой соответствует:
, выбирают строку, которой соответствует:



Если

i – порождающая строка:
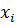 +
+  + … +
+ … +  +…+
+…+ 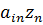 =
= 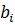
(1+0)  + ([
+ ([  ] +
] +  )
)  + … + ([
+ … + ([  ] +
] +  )
) 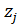 + … ([
+ … ([  ] +
] + 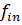 )
)  = [
= [ 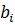 ] +
] + 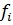
- [0 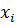 +
+ 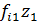 + … +
+ … +  + … + … + … +
+ … + … + … +  ]+
]+  = -
= - 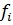
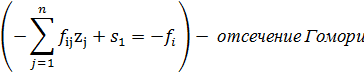


ЗЦП не имеет решения, если в симплекс-таблице появляется, хотя бы одна строка с дробным свободным членом ( ) и целыми коэффициентами
) и целыми коэффициентами  при переменных
при переменных  (
( ) (в этом случае соответствующие уравнение не имеет решения в целых числах).
) (в этом случае соответствующие уравнение не имеет решения в целых числах).
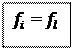 Пример 2:
Пример 2:
| Б
| 
| -3
|
|
|
|
|
| В
| [ 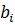 ] ]
| 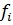
| 
| 
|
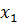
| 
| 
| 
| 
| 
|

|
| -1/4
|
| 3/4
|
|
| 3/2
| 9/2
|
| 1/2
|
| 1/4
|

|
| 3/4
|
| 1/2
|
|
| -1/2
| 7/2
|
| 1/2
| 7/4
| 2/7
|

|
| -3/4
|
| 1/4
|
|
| -1/4
|
|
|
| -
| -
|

|
|
|
|
|
|
|
| -
| -
| -
| -
|
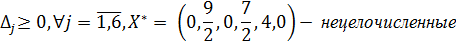


Строка, соответствующая  – порождающая:
– порождающая:




отсечение Гомори (для дальнейшего решения применяют двойственный симплекс – метод)
Пример 1 (продолжение).

| Б
| 
|
|
|
|
|  В В
| [ 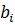 ] ]
|  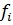
| 
| 
|
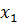
| 
| 
| 
|

|
|
|
| 7/22
| 1/22
| 7/2
|
| 1/2
| 8/22
|  11/8 11/8
|
|
|
|
| -1/22
| 3/22
| 9/2
|
| 1/2
| 24/22
| 11/24
|

|
|
| 28/11
| 15/11
|  63 63
| -
|  - -
|
|
|


| Б
| 
|
|
|
|
|
| В
|

| 
| 
| 
| 
|

|
|
|
| 7/22
| 1/22
|
| 7/2
|

|
|
|
| -1/22
| 3/22
|
| 9/2
|

|
|
|
| -7/22
| -1/22
|
| -1/2
|
|
|
| 28/11
| 15/11
|
|
|

|
|
|
|
|
|
|  3 3
|

|
|
|
|
| 1/7
| -1/7
|  32/7 32/7
|
|
|
|
|
| 1/7
| -22/7
| 11/7
|
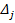
|
|
|
|
|
|
|



| Б
| 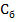
|
|
|
|
|
|
| В
|

| 
| 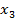
| 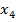
| 
| 
|

|
|
|
|
|
|
|
|
|

|
|
|
|
| 1/7
| -1/7
|
| 32/7
|

|
|
|
|
| 1/7
| -22/7
|
| 11/7
|

|
|
|
|
| -1/7
| -6/7
|
| -4/7
|
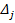
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|

|
|
|
|
|
| -1
|
|
|
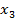
|
|
|
|
|
| -4
|
|
|
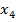
|
|
|
|
|
|
| -7
|
|
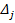
|
|
|
|
|
|
|
|
II. Частично целочисленная задача: 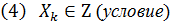
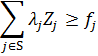
Пусть в примере (А) 
 Z (условие целочисленности накладывается только на
Z (условие целочисленности накладывается только на
 , все остальные
, все остальные  , j≠2, могут быть дробными)
, j≠2, могут быть дробными)
Пример 3: 
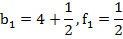
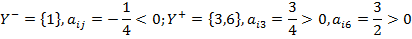
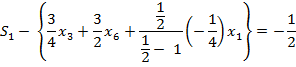

 i – порождающая строка:
i – порождающая строка:



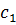


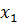
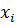




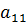
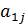






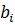


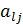

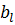


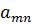





 Б (небазисные)
Б (небазисные)
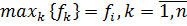

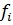 =
= 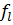 , выбирают строку, которой соответствует:
, выбирают строку, которой соответствует:


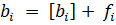




 + … +
+ … +  +…+
+…+ 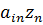 =
=  + ([
+ ([  )
)  + … + ([
+ … + ([  )
) 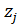 + … ([
+ … ([ 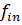 )
)  = [
= [ 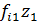 + … +
+ … +  + … + … + … +
+ … + … + … +  ]+
]+  = -
= - 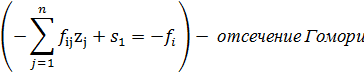


 ) и целыми коэффициентами
) и целыми коэффициентами  при переменных
при переменных  (
( ) (в этом случае соответствующие уравнение не имеет решения в целых числах).
) (в этом случае соответствующие уравнение не имеет решения в целых числах).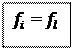 Пример 2:
Пример 2:







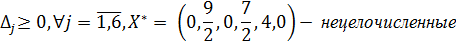







 В
В



 11/8
11/8
 63
63
 -
-




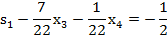


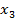
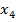

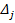
 3
3
 32/7
32/7




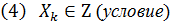
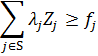



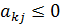

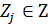

 Z (условие целочисленности накладывается только на
Z (условие целочисленности накладывается только на