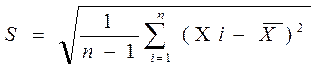Методика обработки результатов эксперимента

 

При обработке результатов эксперимента необходимо:

1. исключить грубые ошибки из ряда наблюдений;

2. вычислить необходимые статистики для характеристики результатов опытов;

3. проверить значимость разницы между оценками математического ожидания различных опытов;

4. представить в той или иной форме результаты опытов.

Исключить грубые ошибки из ряда наблюдений: Грубой ошибкой, или промахом считают заведомо неверный результат измерения. Грубые ошибки возникают вследствие нарушения основных условий наблюдения, резко­го, непредусмотренного изменения условий проведения, экс­перимента или же в результате описок, неверных записей и т. д. Поэтому, результат измерения, содержащий грубую ошибку, должен резко отличаться от всех остальных. На этом обстоятельстве и основаны критерии исключения грубых ошибок.

Для того чтобы исключить грубую ошибку, не полагаясь на интуицию, следует рассчитать величину

t=(x_(!)-x)/S

где х_(!) —подозреваемый на грубую ошибку результат;

 

 

 

S --среднее квадратичное отклонение, рассчитываемое по формуле и затем сравнить полученное значение!t! с критическим значением t_k;p, полученным из (как уже отмечалось выше, значение р выбирается в соответствий с требованиями, предъявляемыми к результату, т. е. в зависимости от того, с какой надежностью мы хотим иметь серию наблюдений, не содержащую грубых ошибок. Если!t! > t _{k; р}, то с вероятностью р можно считать, что результат содержит грубую ошибку, и исключить ее из дальнейшей обработки.

Однако и этим способом надо пользоваться осторожно и отдавать отчет в том, что даже, применяя такой критерий, можно исключить верное измерение.

Вычисление необходимых статистик для характеристики результатов опытов:и каким-либо образом сравнить полученные экспериментальные данные, в каждом опыте, состоящем из п наблюдений, нужно рассчитать следующие статистики:

1.Оценку математического ожидания выходного параметра (среднее арифметическое значение) х;

2.Выборочное среднее квадратичное отклонение S.

Эта статистика и является оценкой случайной ошибки наблюдения.

3.Коэффициент вариации V. Эта статистика также служит для характеристики рассеяния результатов опыта и вычисляется по формуле

 

V=S/x 100%.

Коэффициент вариации лучше использовать для характеристики опытов с различными средними, но он, являясь относительной характеристикой, как бы разрешает большую ошибку для большего среднего, и иногда это надо учитывать особо;

4.Выборочное среднее квадратичное отклонение среднего значения Sx. и является оценкой случайной ошибки результата опыта;

5.Квантиль распределения Стьюдента t_k;p. Для соответствующего числа степеней свободы k=n—1 и доверительной вероятности р принимается по таблице;