ОБРАБОТКА ЭКСПЕРТНЫХ ОЦЕНОК
§ 5.1. Задачи обработки
После проведения опроса группы экспертов осуществляется обработка результатов. Исходной информацией для обработки являются числовые данные, выражающие предпочтения экспертов, и содержательное обоснование этих предпочтений. Целью обработки является получение обобщенных данных и новой информации, содержащейся в скрытой форме в экспертных оценках. На основе результатов обработки формируется решение проблемы. Наличие как числовых данных, так и содержательных высказываний экспертов приводит к необходимости применения качественных и количественных методов обработки результатов группового экспертного оценивания. Удельный вес этих методов существенно зависит от класса проблем, решаемых экспертным оцениванием. Как отмечалось в первой главе, все множество проблем можно разделить на два класса. К первому классу относятся проблемы, для решения которых имеется достаточный уровень знании и опыта, т. е. имеется необходимый информационный потенциал. При решении проблем, относящихся к этому классу, эксперты рассматриваются как хорошие в среднем измерители. Под термином «хорошие в среднем» понимается возможность получения результатов измерения, близких к истинным. Для множества экспертов их суждения группируются вблизи истинного значения. Отсюда следует, что для обработки результатов группового экспертного оценивания проблем первого класса можно успешно применять методы математической статистики, основанные на осреднении данных. Ко второму классу относятся проблемы, для решения которых еще не накоплен достаточный информационный потенциал. В связи с этим суждения экспертов могут очень сильно различаться друг от друга. Более того, суждение одного эксперта, сильно отличающееся от остальных мнений, может оказаться истинным. Очевидно, что применение методов осреднения результатов групповой экспертной оценки при решении проблем второго класса может привести к большим ошибкам. Поэтому обработка результатов опроса экспертов в этом случае должна базироваться на методах, не использующих принципы осреднения, а на методах качественного анализа. Учитывая, что проблемы первого класса являются наиболее распространенными в практике экспертного оценивания, основное, внимание в этой главе уделяется методам обработки результатов экспертизы для этого класса проблем. В зависимости от целей экспертного оценивания и выбранного метода измерения при обработке результатом опроса возникают следующие основные задачи: построение обобщенной оценки объектов па основе индивидуальных оценок экспертов; построение обобщенной оценки на основе парного сравнения объектов каждым экспертом; определение относительных весов объектов; определение согласованности мнений экспертов; определение зависимостей между ранжировками; оценка надежности результатов обработки. Задача построения обобщенной оценки объектов по индивидуальным оценкам экспертов возникает при групповом экспертном оценивании. Решение этой задачи зависит от использованного экспертами метода измерения. При решении многих задач недостаточно осуществить упорядочение объектов по одному показателю или некоторой совокупности показателей. Желательно иметь численные значения для каждого объекта, определяющие относительную его важность по сравнению с другими объектами. Иными славами, для многих задач необходимо иметь оценки объектов, которые не только осуществляют их упорядочение, но и позволяют определять степень предпочтительности одного объекта перед другим. Для решения этой задачи можно непосредственно применить метод непосредственной оценки (см. параграф 2.3). Однако эту же задачу при определенных условиях можно решить путем обработки оценок экспертом. Определение согласованности мнении экспертов производится путем вычисления числовой меры, характеризующей степень близости индивидуальных мнений. Анализ значения меры согласованности способствует выработке правильного суждения об общем уровне знаний по решаемой проблеме и выявлению группировок мнений экспертов. Качественный анализ причин группировки мнений позволяет установить существование различных взглядов, концепций, выявить научные школы, определить характер профессиональной деятельности и т. п. Все эти факторы дают возможность более глубоко осмыслить результаты опроса экспертов. Обработкой результатов экспертного оценивания можно определять зависимости между ранжировками различных экспертов и тем самым устанавливать единство и различие в мнениях экспертов. Важную роль играет также установление зависимости между ранжировками, построенными по различным показателям сравнения объектов. Выявление таких зависимостей позволяет вскрыть связанные показатели сравнения и, может быть, осуществить их группировку по степени связи. Важность задачи определения зависимостей для практики очевидна. Например, если показателями сравнения являются различные цели, а объектами — средства достижения целей, то установление взаимосвязи между ранжировками, упорядочивающими средства с точки зрения достижения целей, позволяет обоснованно ответить на вопрос, в какой степени достижение одной цели при данных средствах способствует достижению других целей. Оценки, получаемые на основе обработки, представляют собой случайные объекты, поэтому одной из важных задач процедуры обработки является определение их надежности. Решению этой задачи должно уделяться соответствующее внимание. Обработка результатов экспертизы представляет собой трудоемкий процесс. Выполнение операций вычисления оценок и показателей их надежности вручную связано с большими трудовыми затратами даже в случае решения простых задач упорядочения. В связи с этим целесообразно использовать вычислительную технику и особенно ЭВМ. Применение ЭВМ выдвигает проблему разработки машинных программ, реализующих алгоритмы обработки результатов экспертного оценивания. § 5.2. Групповая оценка объектов В данном параграфе рассматриваются алгоритмы обработки результатов экспертного оценивания множества объектов. Пусть m экспертов произвели оценку п объектов по l показателям. Результаты оценки представлены в виде величин Рассмотрим вначале случай, когда величины
где
Коэффициенты весов показателем могут быть определены экспертным путем. Если
Получение групповой экспертной оценки путем суммирования индивидуальных оценок с весами компетентности и важности показателей при измерении свойств объектов в кардинальных шкалах основывается на предположении о выполнении аксиом теории полезности фон Неймана — Моргенштерна как для индивидуальных, так и для групповой оценки [39] и условий неразличимости объектов в групповом отношении, если они неразличимы во всех индивидуальных оценках (частичный принцип Парето) [31]. В реальных задачах эти условия, как правило, выполняются, поэтому получение групповой оценки объектов путем суммирования с весами индивидуальных оценок экспертов широко применяется на практике. Коэффициенты компетентности экспертов можно вычислить по апостериорным данным, т. е. по результатам оценки объектов. Основной идеей этого вычисления является предположение о том, что компетентность экспертов должна оцениваться по степени согласованности их оценок с групповой оценкой объектов. Алгоритм вычисления коэффициентов компетентности экспертов имеет вид рекуррентной процедуры:
Вычисления начинаются с t=1. В формуле (5.4) начальные значения коэффициентов компетентности принимаются одинаковыми и равными kj°=1/m. Тогда по формуле (5.4) групповые оценки объектов первого приближении равны средним арифметическим значениям оценок экспертов
Далее вычисляется величина λ¹ по формуле (5.5):
и значение коэффициентов компетентности первого приближения по формуле (5.6):
Используя коэффициенты компетентности первого приближения, можно повторить весь процесс вычисления по формулам (5.4), (5.5), (5.6) и получить вторые приближения величин Повторение рекуррентной процедуры вычислений оценок объектов и коэффициентов компетентности естественно ставит вопрос о ее сходимости. Для рассмотрения этого вопроса исключим из уравнений (5.4), (5.6) переменные
где матрицы В размерности n∙n и С размерности m∙m равны
Величина Если матрицы В и С неотрицательны и неразложимы, то как это следует из теоремы Перрона-Фробениуса [33], при t→∞ векторы
Предельные значения векторов x и k можно вычислить из уравнений:
где Условие неотрицательности матриц В и С легко выполняется выбором неотрицательных элементов Условие неразложимости матриц В и С практически выполняется, поскольку, если эти матрицы разложимы, то это означает, что эксперты и объекты распадаются на независимые группы. При этом каждая группа экспертов оценивает только объекты своей группы. Естественно, что получать групповую оценку в этом случае нет смысла. Таким образом, условия неотрицательности и неразложимости матриц В и С, а следовательно, и условия сходимости процедур (5.4), (5.5), (5.6) в практических условиях выполняются. Следует заметить, что практическое вычисление векторов групповой оценки объектов и коэффициентов компетентности проще выполнять по рекуррентным формулам (5.4), (5.5), (5.6). Определение предельных значений этих векторов по уравнению (5.13) требует применения вычислительной техники. Пример. Три эксперта (m = 3) оценили значение двух мероприятий (n=2) по решению одной проблемы (l =1), приведя нормированные оценки Проведем вычисление групповых оценок мероприятий и коэффициентов компетентности экспертов по формулам (5.4), (5.5), (5.6). Средние оценки объектов первого приближения по формуле (5.4) при t=1 равны
Вычислим величину λ¹ по формуле (5.5). В результате имеем λ¹=1∙0,335+2∙0,665=1,665. Вычисляем коэффициенты компетентности первого приближения по формуле (5.6):
Вычисляя групповые оценки объектов второго приближения, получаем вектор x²=(0.324; 0.676). Величина λ²=1,676. Вектор коэффициентов компетентности второго приближения равен k²=(0,341; 0,298; 0,361). Для третьего приближения получаем x³=(0,3233; 0,6765), λ³=1,6765, k³=(0,341; 0,298; 0,361). Как следует из результатов третьего приближения, вектор коэффициентов компетентности стабилизировался. Поэтому дальнейшие вычисления не дадут существенного уточнения. Рассмотрим теперь вычисление предельных значений векторов групповой оценки и коэффициентов компетентности по уравнениям (5.13). Вычисляя матрицу В=ХХ’, получаем
Максимальное собственное число матрицы В определяется как максимальный корень уравнения |В-λE |=0, где Е – единичная матрица. Записывая в явном виде определитель, получаем
Раскрывая определитель, получаем квадратное уравнение λ² - 1,76λ + 0,14 = 0. Максимальный корень этого yравнения ранен λo=l,676. Сравнивая это значение со вторым и третьим приближением λ², λ³, убеждаемся в том, что они близки. Вектор групповых оценок вычисляется путем решения системы уравнений
Решая эту систему yравнений, получаем Вычисляя матрицу С = Х'Х, получаем
Составляя уравнение |С — XE|=0 и раскрывая определитель, получаем уравнение λ(λ²-1,76λ+0,14)=0. Отсюда следует, что максимальное собственное число для матрицы С совпадает с максимальным собственным числом матрицы В: λо=1,676. Система уравнений для определения предельных коэффициентов компетентности имеет вид
Решая эту систему уравнений, получаем Рассмотрим теперь случай, когда эксперты производят оценку множества объектов методом ранжирования так, что величины Ранжировку Rj можно представить в виде матрицы парных сравнений, элементы которой определим следующим образом:
Очевидно, что Если все ранжируемые объекты эквивалентны, то все элементы матрицы парных сравнений равны нулю. Такую матрицу будем обозначать Ro и считать, что точка в пространстве ранжировок, соответствующая матрице Rоявляется началом отсчета. Обращение порядка ранжируемых объектов приводит к транспонированию матрицы парных сравнений. Метрика d(Ri, Rj) как расстояние между i-йи j-й ранжировками определяется единственным образом формуллой
если выполнены следующие 6 аксиом [26]: 1. d(Ri, Rj)≥0, причем равенство достигается, если ранжировки Ri и Rj тождественны; 2. d(Ri, Rj)= d(Rj, Ri); 3. d(Ri, Rh)+ d(Rh, Rj)≥ d(Ri, Rj); причем равенство достигается, если ранжировка «лежит между» ранжировками Ri и Rj. Понятие «лежит между» означает, что суждение о некоторой паре OhOl объектов в ранжировке совпадает с суждением об этой паре либо в Ri, либо в Rj или же в Ri Ok > О l, в Rj О l > Ok, а в Rh Oh ∞ О l; 4. d(R'i, R'j)= d(Ri, Rj), где R'i получается из Ri некоторой перестановкой объектов, а R'j из Rj той же самой перестановкой. Эта аксиома утверждает независимость расстояния от перенумерации объектов. 5. Если две ранжировки Ri, Rj одинаковы всюду, за исключением n-элементного множества элементов, являющегося одновременно сегментом обеих ранжировок, то d(Ri,Rj) можно вычислить, как если бы рассматривалась ранжировка только этих n-объектов. Сегментом ранжировки называется множество, дополнение которого непусто и все элементы этого дополнения находятся либо впереди, либо позади каждого элемента сегмента. Смысл этой аксиомы состоит в том, что если две ранжировки полностью согласуются в начале и конце сегмента, а отличие состоит в упорядочении средних n-объектов, то естественно принять, что расстояние между ранжировками должно равняться расстоянию, соответствующему ранжировкам средних n-объектов.
Пространство ранжировок при двух объектах можно изобразить в виде трех точек, лежащих на одной прямой (рис.3). Расстояния между точками равны d(R1, 0)= d(R2, 0)=1, d(R1, R2)=2. При трех объектах пространство всех возможных ранжировок состоит из 13 точек. Это пространство изображено на рис.4.
Рис.4. Используя введенную метрику, определим обобщенную ранжировку как такую точку, которая наилучшим образом согласуется с точками, представляющими собой ранжировки экспертов. Понятие наилучшего согласования на практике чаще всего определяют как медиану и среднюю ранжировку. Медиана есть такая точка в пространстве ранжировок, сумма расстояний от которой до всех точек — ранжировок экспертов является минимальной. В соответствии с определением медиана вычисляется из условия
Средняя ранжировка есть такая точка, сумма квадратов расстояний от которой до всех точек — ранжировок экспертов является минимальной. Средняя ранжировка определяется из условия
Пространство ранжировок конечно и дискретно, поэтому медиана и средняя ранжировка могут быть только какими-либо точками этого пространства. В общем случае медиана и средняя ранжировка могут не совпадать ни с одной из ранжировок экспертов. Если учитывается компетентность экспертов, то медиана и средняя ранжировка определяются из условий:
где kj — коэффициенты компетентности экспертов. Если ранжировка объектов производится по нескольким показателям, то определение медианы вначале производится для каждого эксперта по всем показателям, а затем вычисляется медиана по множеству экспертов:
где qh – коэффициенты весов показателей. Основным недостатком определения обобщенной ранжировки в виде медианы или средней ранжировки является трудоемкость расчетов. Естественный способ отыскания Rм или Rc в виде перебора всех точек пространства ранжировок неприемлем вследствие очень быстрого роста разномерности пространства при увеличении количества объектов и, следовательно, роста трудоемкости вычислений. Можно свести задачу отыскания Rм или Rс к специфической задаче целочисленного программирования. Однако это не очень эффективно уменьшает вычислительные трудности. Пример. Проиллюстрируем применение понятий медианы и среднего значения на простом примере, когда имеются три объекта (n=3) и ранжировка произведена тремя экспертами (m=3). Результаты ранжировки проставлены в табл. 5.2. ТАБЛИЦА 5.2
На основе этой таблицы составим матрицы парных сравнений
При n=3 пространство ранжировок может иметь 13 несовпадающих точек (рис. 4). Представим три точки R1=R2= Rз, соответствующие ранжировкам данного примера, и ближайшие к ним точки на рис. 5. Нетрудно непосредственным расчетом убедиться, что медианой является точка R1=R2. Действительно, сумма расстояний от медианы до трех точек R1, R2, Rз равна d(R1, RM)+d(R2, RM)+d(Rз, Rм) = 0+0+2=2. Если выбрать медиану в любой другой точке, то сумма расстояний будет больше 2. Например, если выбрать в качестве медианы точку А, соответствующую ранжировке О1 ∞ О2 >О3, то сумма расстояний равна d(R1, A)+d(R2, А)+d(R3, A) = 1 + 1 + 1=3. Таким образом, медианой является точка R1 = R2 или, иными словами, в качестве обобщенной ранжировки следует выбрать ранжировку, выполненную первым или вторым экспертом. В данном случае обобщенная ранжировка определена по правилу большинства голосов. Рассмотрим, какая ранжировка будет соответствовать среднему значению. Непосредственным расчетом нетрудно убедиться, что среднее значение соответствует точке А. действительно, сумма квадратов расстояний от точки А до точек R1, R2, R3 равна d²(R1, А)+ d²(R2, А)+ d²(R3, А)=1² + 1² + 1² = 3. Если взять в качестве среднего значения медиану (точка R1 = R2), то сумма квадратов равна d²(R1, RМ)+ d²(R2, RМ)+ d²(R3, RМ)=0² + 0² + 2² = 4. Эта величина больше, чем в предыдущем случае. Таким образом, построение обобщенной ранжировки по среднему значению дает ранжировку О1 ∞ О2 >О3. Эта ранжировка не совпадает ни с одной из ранжировок R1, R2, Rз, выполненных экспертами. Ранжировку О1 ∞ О2 >О3 можно интерпретировать как эквивалентность первого и второго объектов и их предпочтительность перед третьим объектом. Обобщенные ранжировки по критериям медианы и среднего значения согласуются в отношении О3 — он на последнем месте, что соответствует оценкам всех трех экспертов. В отношении объектов О1, О2 критерии медианы и среднего значения дают разногласие. Критерий медианы утверждает, что нужно следовать правилу большинства, тогда как критерий среднего значения решает, что это неубедительно и необходимо считать эти объекты равноценными. С практической точки зрения оба эти результата являются приемлемыми. Рассмотрим случай, когда все три эксперта дают различные ранжировки R1=(O1 > О2 > О3), R2 =(О2> O3>O1), Rз =(Оз> O1 > О2). Анализируя расположение этих точек на рис. 5, нетрудно определить, что медианой будет не одна, а три точки, совпадающие с точками R1, R2, Rз. Сумма расстояний от медиан до точек R1, R2, Rз одинакова и равна d(R1, RМ)+ d(R2, RМ)+ d(R3, RМ)=8. Средним значением будет одна центральная точка Rc= (O1 ∞ О2 ∞ О3). Сумма квадратов расстояний от среднего значения до точек R1, R2, Rз равна d²(R1, Rс)+ d²(R2, Rс)+ d²(R3, Rс)=3² + 3² + 3² = 27.
Рис.5. Таким образом, критерий медианы утверждает в данном случае, что в качестве обобщенной ранжировки можно принять любую ранжировку экспертов. Критерий среднего значения решает, что все объекты равноценны. С практической точки зрения представляется, что критерий среднего значения дает более приемлемые результаты.
Расхождение обобщенных ранжировок при различных критериях возникает при малом числе экспертов и несогласованности их оценок. Если мнения экспертов близки, то обобщенные ранжировки, построенные по критериям медианы и среднего значения, будут совпадать. Сложность вычисления медианы или средней ранжировки привела к необходимости применения более простых способов построения обобщенной ранжировки. К числу таких способов относится способ сумм рангов. Этот способ заключается в ранжировании объектов по величинам сумм рангов, полученных каждым объектом от всех экспертов. Для матрицы ранжировок
Далее объекты упорядочиваются по цепочке неравенств Пример. Результаты ранжировки пяти объектов пятью экспертами представлены в табл. 5.3.
ТАБЛИЦА 5.3
Результаты вычисления сумм рангов для всех объектов приведены в последней строке таблицы. Из сравнения сумм рангов получаем цепочку неравенств
Отсюда следует обобщенная ранжировка
В данном примере рассмотрен случай, когда отношение между объектами является отношением строгого порядка. Если имеет место и отношение эквивалентности, то процедура построения обобщенной ранжировки по сумме рангов не изменяется. Для учета компетентности экспертов достаточно умножить каждую i-ю ранжировку на коэффициент компетентности j-го эксперта
Обобщенная ранжировка с учетом компетентности экспертов строится на основе упорядочения сумм рангов для всех объектов. Следует отметить, что построение обобщенной ранжировки по суммам рангов является корректной процедурой, если ранги назначаются как места объектов в виде натуральных чисел 1, 2,..., п. Если назначать ранги произвольным образом, как числа в шкале порядка, то сумма рангов, вообще говоря, не сохраняет условие монотонности преобразования и, следовательно, можно получать различные обобщенные ранжировки при различных отображениях объектов на числовую систему. Нумерация мест объектов может быть произведена единственным образом с помощью натуральных чисел. Поэтому при хорошей согласованности экспертов построение обобщенной ранжировки по методу сумм рангов дает результаты, согласующиеся с результатами вычисления медианы. Еще одним более обоснованным в теоретическом отношении подходом к построению обобщенной ранжировки является переход от матрицы ранжировок к матрице парных сравнений и вычисление собственного вектора, соответствующего максимальному собственному числу этой матрицы. Упорядочение объектов производится по величине компонент собственного вектора. Изложение этого подхода дается в параграфе 5.4. § 5.3. Оценка согласованности мнений экспертов При ранжировании объектов эксперты обычно расходятся в мнениях по решаемой проблеме. В связи с этим возникает необходимость количественной оценки степени согласия экспертов. Получение количественной меры согласованности мнений экспертов позволяет более обоснованно интерпретировать причины в расхождении мнений. В настоящее время известны две меры согласованности мнений группы экспертов: дисперсионный и энтропийный коэффициенты конкордации. Дисперсионный коэффициент конкордации [45]. Рассмотрим матрицу результатов ранжировки п объектов группой из m экспертов
Величины
где
Дисперсионный коэффициент конкордации определяется как отношение оценки дисперсии (5.15) к максимальному значению этой оценки
Коэффициент конкордации изменяется от нуля до единицы, поскольку Вычислим максимальное значение оценки дисперсии для случая отсутствия связанных рангов (все объекты различны). Предварительно покажем, что оценка математического ожидания зависит только от числа объектов и количества экспертов. Подставляя в (5.16) значение
Рассмотрим вначале суммированные по i при фиксированном j. Это есть сумма рангов для j-го эксперта. Поскольку эксперт использует для ранжировки натуральные числа от 1 до п, то, как известно, сумма натуральных чисел от 1 до п равна
Подставляя (5.19) в (5.18), получаем
Таким образом, среднее значение зависит только от числа экспертов m и числа объектов п. Для вычисления максимального значения оценки дисперсии подставим в (5.15) значение
Учитывая, что из (5.18) следует
получаем
Максимальное значение дисперсии достигается при наибольшем значении первого члена в квадратных скобках. Величина этого члена существенно зависит от расположения рангов — натуральных чисел в каждой строке i. Пусть, например, все т экспертов дали одинаковую ранжировку для всех п объектов. Тогда в каждой строке матрицы
Возводя в квадрат и суммируя по i, получаем значение первого члена в (5.22):
Теперь предположим, что эксперты дают несовпадающие ранжировки, например, для случая п = т все эксперты присваивают разные ранги одному объекту. Тогда
Сравнивая это выражение с Таким образом, случай полного совпадения ранжировок экспертов соответствует максимальному значениютоценки дисперсии. Подставляя (5.23) в (5.22) и выполняя преобразования, получаем
Введем обозначение
Используя (5.25), запишем оценку дисперсии (5.15) в виде
Подставляя (5.24), (5.25), (5.26) в (5.17) и сокращая на множитель (п —1), запишем окончательное выражение для коэффициента конкордации
Данная формула определяет коэффициент конкордации для случая отсутствия связанных рангов. Если в ранжировках имеются связанные ранги, то максимальное значение дисперсии в знаменателе формулы (5.17) становится меньше, чем при отсутствии связанных рангов. Можно показать, что при наличии связанных рангов коэффициент конкордации вычисляется по формуле [21]:
где
В формуле (5.28)
|

 , где j —номер эксперта, i — номер объекта, h — номер показателя (признака) сравнения. Если оценка объектов произведена методом ранжирования, то величины
, где j —номер эксперта, i — номер объекта, h — номер показателя (признака) сравнения. Если оценка объектов произведена методом ранжирования, то величины  (i=1, 2, …, n), (5.1)
(i=1, 2, …, n), (5.1) — коэффициенты весов показателей сравнения объектов, kj — коэффициенты компетентности экспертов. Коэффициенты весов показателей и компетентности объектов являются нормированными величинами
— коэффициенты весов показателей сравнения объектов, kj — коэффициенты компетентности экспертов. Коэффициенты весов показателей и компетентности объектов являются нормированными величинами (5.2)
(5.2) — коэффициент веса h-го показателя, даваемый j-м экспертом, то средний коэффициент веса h- гопоказателя по всем экспертам равен
— коэффициент веса h-го показателя, даваемый j-м экспертом, то средний коэффициент веса h- гопоказателя по всем экспертам равен (5.3)
(5.3) ; (5.4)
; (5.4) ; (5.5)
; (5.5) . (5.6)
. (5.6) . (5.7)
. (5.7) (5.8)
(5.8)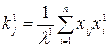 (5.9)
(5.9) .
. и
и  и представим эти уравнения в векторной форме
и представим эти уравнения в векторной форме , (5.10)
, (5.10) . (5.11)
. (5.11) в уравнениях (5.10) определяется по формуле (5.5).
в уравнениях (5.10) определяется по формуле (5.5). и
и  сходятся к собственным векторам матриц В и С, соответствующим максимальным собственным числам этих матриц
сходятся к собственным векторам матриц В и С, соответствующим максимальным собственным числам этих матриц ,
,  . (5.12)
. (5.12) (5.13)
(5.13) ,
,  — максимальные собственные числа матриц В и С.
— максимальные собственные числа матриц В и С. матрицы X оценок объектов экспертами.
матрицы X оценок объектов экспертами. мероприятий (табл. 5.1).
мероприятий (табл. 5.1). .
. ;
; ;
; .
. .
. .
. .
. =0,3235,
=0,3235,  =0,6765, что соответствует результатамрекуррентных вычислений третьего приближения.
=0,6765, что соответствует результатамрекуррентных вычислений третьего приближения. .
. .
. =0,34077,
=0,34077,  =0,298,
=0,298,  =0,36123. Эти значения близки к третьему приближению коэффициентов компетентности.
=0,36123. Эти значения близки к третьему приближению коэффициентов компетентности.
 , поскольку каждый объект эквивалентен самому себе. Элементы матрицы ||
, поскольку каждый объект эквивалентен самому себе. Элементы матрицы ||  || антисимметричны
|| антисимметричны  .
. ,
, 6. Минимальное расстояние равно единице.
6. Минимальное расстояние равно единице.
 .
. .
. ;
;  .
. (i=1,2,…,m);
(i=1,2,…,m); ,
,







 ,
,  ,
,  :
: ,
,  ,
,  .
.
 составляются суммы
составляются суммы (i=1,2,…,n).
(i=1,2,…,n). .
.





 .
. . В этом случае вычисление суммы рангов для i-го объекта производится по следующей формуле:
. В этом случае вычисление суммы рангов для i-го объекта производится по следующей формуле: (i=1,2,…,n).
(i=1,2,…,n). — ранг, присваиваемый j-м экспертом i-му объекту. Составим суммы рангов по каждому столбцу. В результате получим вектор с компонентами
— ранг, присваиваемый j-м экспертом i-му объекту. Составим суммы рангов по каждому столбцу. В результате получим вектор с компонентами рассмотрим как реализации случайной величины и найдем оценку дисперсии. Как известно, оптимальная по критерию минимума среднего квадрата ошибки оценка дисперсии определяется формулой [17]:
рассмотрим как реализации случайной величины и найдем оценку дисперсии. Как известно, оптимальная по критерию минимума среднего квадрата ошибки оценка дисперсии определяется формулой [17]: , (5.15)
, (5.15) - оценка математического ожидания, равная
- оценка математического ожидания, равная . (5.16)
. (5.16) . (5.17)
. (5.17) .
. (5.18)
(5.18) (5.19)
(5.19) . (5.20)
. (5.20) . (5.21)
. (5.21) ,
, . (5.22)
. (5.22) .
. . (5.23)
. (5.23) .
. при т = п, убеждаемся, что первый член в квадратных скобках формулы (9) равен второму члену и, следовательно, оценка дисперсии равна нулю.
при т = п, убеждаемся, что первый член в квадратных скобках формулы (9) равен второму члену и, следовательно, оценка дисперсии равна нулю. . (5.24)
. (5.24) . (5.25)
. (5.25) . (5.26)
. (5.26) . (5.27)
. (5.27) , (5.28)
, (5.28) . (5.29)
. (5.29) - показатель связанных рангов в j-й ранжировке,
- показатель связанных рангов в j-й ранжировке,  - число групп равных рангов в j-й ранжировке,
- число групп равных рангов в j-й ранжировке, 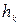 - число равных рангов в k-й группе связанных рангов при ранжировке j-м экспертом. Если совпадающих рангов нет, то
- число равных рангов в k-й группе связанных рангов при ранжировке j-м экспертом. Если совпадающих рангов нет, то 


