Глава 6. Одним из наиболее эффективных методов анкетирования является метод Дельфы [19, 42]
ПРИМЕНЕНИЕ МЕТОДА ЭКСПЕРТНЫХ ОЦЕНОК
§6.1. Метод Дельфы
Одним из наиболее эффективных методов анкетирования является метод Дельфы [19, 42]. Основными особенностями этого метода являются: полный отказ от личных контактов экспертов и коллективных обсуждений; многотуровая процедура опроса экспертов; обеспечение экспертов информацией, включая и обмен информацией между ними, после каждого тура опроса при сохранении анонимности оценок, аргументации и критики; обоснование ответов экспертов по запросу организаторов. Процедура опроса по методу Дельфы заключается и анкетировании экспертом с помощью опросных листов или внешних устройств ЭВМ в несколько туров с обработкой результатов анкетирования в каждом туре и информированием экспертов об этих результатах. На практике обычно ограничиваются четырьмя турами. В первом туре опроса эксперты дают свои ответы без аргументирования. Ответы обрабатываются с целью выделения среднего и крайних мнений. Экспертам сообщаются эти мнения, и проводится второй тур опроса, в ходе которого они пересматривают и при желании изменяют ответы, данные в первом туре. Кроме того, эксперты должны объяснить, почему они изменили или не изменили ответы. Полученные после второго тура новые средние и крайние мнения, а также вся аргументация с сохранением анонимности сообщаются экспертам, и проводится Обычно после третьего или четвертого туров опроса ответы экспертов перестают изменяться, что и является сигналом к прекращению опросов. Такая процедура позволяет экспертам учесть обстоятельства, которыми они пренебрегали или о которых не были осведомлены. По решению ведущего опрос обоснование могут представлять лишь эксперты, ответы которых сильно отличаются от мнения большинства. Необходимость обоснования мнений вынуждает тех экспертов, у которых нет твердого убеждения в своей правоте, помещать свои ответы вблизи от среднего мнения. В то же время эксперты, которые смогли обосновать свои «крамольные» ответы, несмотря, на новую информацию, придерживаются своих первоначальных взглядов. В ряде случаев образуется две группы существенно различных мнений. Это указывает на наличие двух различных подходов, что может объясняться, например, существованием двух научных школ. Дальнейшее проведение опроса в таком случае, как правило, лишь подтверждает создавшееся положение, так как разрешение разных позиций требует глубоких исследований и не может быть результатом экспертизы. Однако и в этом случае опрос полезен, ибо отчетливо выявляет позиции, точки зрения сторон и их аргументацию, что позволяет поставить дальнейшие исследования проблемы. Организация экспертизы включает основные этапы: предварительную ориентировку экспертов, включающую формулирование проблемы и инструктаж экспертов; формулирование вопросов экспертам в виде, требующем четких количественных и качественных оценок; разработку способов и порядка информационного обеспечения экспертов, включая обмен аргументацией; разработку алгоритмов и порядка промежуточной и окончательной обработки результатов. Пример. Поясним процедуру Дельфы на примере оценки значения некоторой величины N (скажем, стоимости разработки какой-то системы). Пример заимствован из [42]. Первый тур. Каждый эксперт должен дать оценку величины N независимо от других экспертов. Оценки экспертов записываем в порядке возрастания предлагаемых значении. Определяем медиану
Рис. 6.
Третий тур. Сообщаем результаты второго тура экспертам, т. е. новые значения Четвертый тур. Экспертам сообщают квартили нового распределения, контраргументы, высказанные в третьем туре, и просят еще раз пересмотреть оценки. Медиана, получаемая в результате четвертого тура, принимается в качестве оценки величины N, представляющей точку зрения всего коллектива экспертов. Сходимость оценок в многотуровой процедуре можно объяснить следующим образом. Среднее значение оценок первого тура опроса всей группы экспертов Мг находится, очевидно, между средним Ми экспертов, изменивших во втором туре свои оценки, и средним Мн экспертов, не изменивших своих оценок. Обычно Мн оказывается ближе к истинному значению оцениваемой величины, чем Ми, и можно предположить, что истинное значение находится где-то в заштрихованной области (рис. 7). Если в процессе итерации Ми будет перемещаться в направлении Мг, то последнее также будет смещаться вправо, т. е. будет происходить уточнение групповой оценки. Ухудшение конечного результата произойдет с большей вероятностью, лишь если не уверенные в своих оценках эксперты изменят их настолько, что Ми окажется правее Мн. Однако такие скачки в изменении оценок маловероятны [9]. Улучшение групповой оценки в результате итераций, таким образом, основано на двух предположениях: ответы экспертов, не изменяющих своих оценок, лежат ближе к истине, чем первоначальные оценки экспертов, не уверенных в своих ответах; среднее оценок экспертов, изменяющих ответы, движется в результате этих изменений к среднему оценок «уверенных» экспертов. Изменение оценок в среднем в сторону их улучшения можно объяснить использованием экспертами информации, не учтенной в первом туре, но учитываемой в последующих, а также получением новой информации, прежде всего от «уверенных» экспертов. Приведенный пример иллюстрирует лишь возможную процедуру в одной из конкретных наиболее простых применений метода Дельфы. В каждой отдельной экспертизе должна быть выработана конкретная программа ее проведения; учитывающая специфику решаемой проблемы и особенности экспертов. Во многих случаях целесообразны, например, изменения вопросов от тура к туру, индивидуальные обращения к экспертам, предварительная обработка их аргументации перед ее передачей другим экспертам. При дельфийской процедуре наличие в группе мало компетентных экспертов меньше сказывается на точности групповой оценки, чем при анкетировании в один тур за счет получения информации от более компетентных экспертов. Последние в ходе экспертизы также обогащаются информацией и могут скорректировать свои оценки. Важно, что в процессе итераций происходит в неявной форме автоматическая оценка компетентности экспертов и взвешивание их мнений с учетом компетентности. Это тем более полезно, что определение истинной компетентности экспертов до экспертизы, как показано в третьей главе, не может быть достаточно надежным. Хорошими примерами использования метода Дельфы могут служить выполнение долгосрочного прогнозирования развития науки и техники корпорацией РЭНД в 1964 г. и ВИНИТИ Академии наук СССР в 1969 г. В эксперименте корпорации РЭНД опрашивались шесть групп экспертов, составленных из 88 специалистов разных профилей, что позволило построить картину ожидаемых научно-технических достижений до первых десятилетий следующего века. Результаты прогноза представлены на рис. 8 в виде квартилей и медианы времени совершения прогнозируемых событий. Рассмотрим кратко процедуру ВИНИТИ с опросом 100 экспертов (35 докторов наук и 65 кандидатов) для составления прогноза примерно на 50 лет [4]. Анкетирование различных групп экспертов проводилось в шесть этапов, некоторые из которых состояли из нескольких туров. В анкетах первого этапа все эксперты должны были указать, какие научные достижения осуществятся, по их мнению, в прогнозируемый период. На основании обработанных ответов экспертов были выделены для дальнейшего анализа семь достижений. На втором этапе опроса группа экспертов проранжировала выделенные проблемы — научные достижения по их важности для научно-технического прогресса в целом, причем каждый эксперт ранжировал лишь три проблемы, в которых он был наиболее компетентен. Этот этап проводился в несколько туров с вычислением после каждого коэффициента конкордации. Опросы прекращались при удовлетворительном согласовании оценок или при отчетливом выявлении двух групп мнений. На третьем этапе те же эксперты оценивали вероятности свершения проранжированных достижений в каждый из интервалов времени, на которые был разделен прогнозируемый период. Расчет коэффициента конкордации позволил распределить полученные оценки на три категории: хорошо согласующиеся оценки; оценки, образующие две группы мнений; оценки, не входящие в первые две категории. На четвертом этапе авторов оценок второй и третьей категорий просили обосновать оценки и заменили их средними оценками большинства, если обоснование не шло дальше
ссылки на интуицию. При проведении этого тура опасность конформизма очень велика, поэтому экспертам не сообщались оценки большинства. По датам свершения ряда событий согласование вновь не было достигнуто, и для уточнения этих дат был проведен пятый этап опроса. На пятом этапе экспертов, составивших на третьем этапе большинство, просили обосновать свои оценки и опровергнуть мнение меньшинства или же приблизить свои оценки к оценкам последних. Некоторые эксперты этой группы пересмотрели свои оценки, что показало их подверженность влиянию чужих оценок, а отсюда необходимость осторожности при учете их мнения, Все вопросы вновь разделили на вопросы, ответы на которые хорошо согласуются, и вопросы, по которым не достигнуто согласование ответов. Ответы на вопросы второй категории в свою очередь делятся на ответы, четко образующие две группы мнений и измененные в пользу меньшинства ответы экспертов, образовавших большинство на третьем этапе. Ответы первой из этих групп не согласовывались, и по ним составлялись два прогноза. Ответы второй группы подвергались последнему — шестому согласованию, перед которым эксперты, давшие эти ответы, были разделены на группу большинства и группу меньшинства. Последней группе были разосланы анкеты четвертого этапа. В результате шестого этапа опроса были получены достаточно согласованные оценки, и группа управления приступила к окончательной обработке результатов опроса. При обработке итоговые значения вероятностей свершения прогнозируемых событий сводились в анкету третьего этапа и определялись медианы и квартили групповых оценок. Составленный прогноз утверждал, что до второго десятилетия следующего века можно ожидать свершения практически всех выделенных экспертами научных достижений. Сравнение полученного прогноза с прогнозом корпорации РЭНД показало хорошую сходимость ряда оценок времени свершения одинаковых событий. Метод Дельфы обладает определенными недостатками, основными из которых являются большие затраты времени на многотуровую экспертизу, а также полное исключение прямого столкновения мнений экспертов. Длительность процедуры, достигающая при большом числе экспертов многих месяцев, если проводится письменное анкетирование, затрудняет работу экспертов и приводит к нестабильности их состава. Необходимость неоднократного пересмотра оценок также вызывает отрицательную реакцию экспертов, что не может не сказаться на качестве их работы. Резкое сокращение времени проведения экспертизы возможно путем создания автоматизированной системы сбора и обработки мнений экспертов и их информационного обеспечения на основе ЭВМ. Каждый-эксперт передает и получает от ЭВМ информацию с помощью телетайпов и дисплеев. ЭВМ с внешними устройствами обеспечивает контакты между экспертами при сохранении анонимности и регулируемости контактов. Программа работы ЭВМ должна обеспечивать представление вопросов экспертам, сбор ответов, обработку ответов, запрос аргументации экспертов, выдачу аргументации и другой необходимой экспертам информации, анализ и вычисления, нужные экспертам для составления ответов. Недостатки описанной процедуры стимулировали разработку различных модификаций метода Дельфы, из которых следует упомянуть модификацию, получившую название SEER (System for Event Evaluation and Review) — система оценки и обзора события [49]. Метод SEER был разработан и применен для целей прогнозирования техники обработки информации на 15 лет. Метод предусматривает лишь два тура опроса групп экспертов разного состава. В первом туре группа состоит из специалистов фирм — производителей технических средств и математического обеспечения обработки информации. Группа экспертов второго тура состоит из специалистов высшей квалификации в области обработки информации, работающих в организациях, принимающих решения, и ученых — специалистов в области естественных и технических наук. В обоих турах в отличие от «классического» метода Дельфы эксперты возвращаются к рассмотрению поставленных перед ними вопросов только когда их оценки выпадают за интервалы оценок большинства экспертов. В первом туре эксперты — представители фирм составляют список —банк данных о вероятных достижениях и новых разработках в отрасли. Эксперты производят также оценки желательности каждого события для потребителя, оценки технических и экономических возможностей его совершения и определяют три даты свершения события: с минимальной учитываемой вероятностью (вероятность 0,2), вероятного свершения (вероятность 0,5) и почти достоверного свершения (вероятность 0,9). Во втором туре вторая группа экспертов производит переоценку и пополнение банка данных, определяет наиболее важные события, их взаимное влияние и уточняет технический прогноз. В результате второго тура получают список потенциально возможных и желательных событий, используемый для разработки перечня кратко-, средне- и долгосрочных целей и выявления событий, обеспечивающих достижение этих целей.
Рис.9. Второй тур имеет, таким образом, нормативный характер и его результаты могут быть непосредственно использованы для планирования исследований, разработок новой техники и производства. Прогноз оформляется в виде графа взаимодействия целей и событий (рис. 9), представляемого потребителю — органу, планирующему научно-техническое развитие в данной области.
|

 и квартили
и квартили 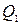 и
и  . В результате каждый из четырех интервалов, образованных точками
. В результате каждый из четырех интервалов, образованных точками 
 Второй тур. Сообщаем экспертам значения
Второй тур. Сообщаем экспертам значения 




