Метод, основанный на преобразовании матрицы предпочтений

На основании матрицы нормализованных рангов (табл. 3) составим матрицу предпочтений А (табл. 8), подсчитав число случаев, когда i -й производитель определялся экспертами как более качественный, чем j -й.

При составлении табл. 8 каждый столбец табл. 3, соответствующий i -му
производителю, сравнивался построчно со столбцом, соответствующим j -му
производителю. Например, при сравнении 1-го и 2-го столбца получаем, что
продукцию производителя 1 сочли более качественной, чем производителя 2

семь экспертов: 2, 3, 6, 11, 12, 13 и 14-й, три эксперта посчитали продукцию
производителей одинаковой по качеству: 1, 8 и 9. Следовательно, в табл. 8 на
пересечении 1-й строки и 2-го столбца должна стоять цифра 8,5. Соответственно, на пересечении 2-й строки и 1-го столбца должна стоять

цифра 14-8,5=5,5.

Таблица 8

Матрица предпочтений А

Производители	Производители
	0,0	8,5	3,5	13,5	14,0	12,5	9,0
	5,5	0,0	3,5	14,0	13,5	11,0	9,0
	10,5	10,5	0,0	14,0	14,0	13,0	13,0
	0,5	0,0	0,0	0,0	9,0	4,0	2,5
	0,0	0,5	0,0	5,0	0,0	4,0	2,0
	1,5	3,0	1,0	10,0	10,0	0,0	5,0
	5,0	5,0	1.0	11,5	12,0	9,0	0,0

 

Разделив каждое из чисел, стоящих в табл. 8, на число экспертов (m = 14),
получаем матрицу Р (табл. 9).

 

Таблица 9

Матрица вероятностей Р

 

Производители	Производители
	0,000	0,607	0,250	0,964	0,964	0,893	0,643
	0,393	0,000	0,250	0,964	0,964	0,786	0,643
	0,750	0,750	0,000	0,964	0,964	0,929	0,929
	0,036	0,036	0,036	0,000	0,643	0,286	0,179
	0,036	0,036	0,036	0,357	0,000	0,286	0,143
	0,107	0,214	0,071	0,714	0,714	0,000	0,357
	0,357	0,357	0,071	0,821	0,857	0,643	0,000

 

При этом значения 0 (кроме диагональных элементов) 0 и 1 в матрице Р заменялись соответственно на и

По данным матрицы вероятностей Р, пользуясь таблицами нормированного нормального распределения [7], составляем матрицу (табл. 10),

элементами которой и являются оценки разностей значений zi и zj характеризующих «истинное» качество соответственно i-го и j-гo производителя. В последнем столбце таблицы 10 записываем суммы элементов по строкам.

 

Таблица 10

Матрица оценок разностей важностей Z

 

Производители	Производители
	0,000	0,272	-0,675	1,790	1,790	1,242	0,366	4,785
	-0,272	0,000	-0,675	1,790	1,790	0,792	0,366	3,791
	0,675	0,675	0,000	1,790	1,790	1,465	1,465	7,860
	-1,790	-1,790	-1,790	0,000	0,366	-0,566	-0,921	-6,491
	-1,790	-1,790	-1,790	-0,366	0,000	-0,566	-1,068	-7,370
	-1,242	-0,792	-1,465	0,566	0,566	0,000	-0,366	-2,733
	-0,366	-0,366	-1,465	0,921	1,068	0,366	0,000	0,158

 

Для нахождения коэффициентов относительной важности βj определяем
значения по формуле (15) и Ф () функцию нормированного нормального
распределения для каждого , а затем нормируем полученные значения Ф()
по формуле (16).

 

 

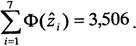
Результаты расчета сводим в табл. 11.

 

Таблица 11

Результаты расчета относительной важности по модели Тэрстоуна

 

Производители		Ф ()	βj
	0,684	0,753	0,215
	0,542	0,706	0,201
	1,123	0,869	0,248
	-0,927	0,177	0,050
	-1,053	0,144	0,041
	-0,390	0,348	0,099
	0,022	0,509	0,145

 

Таким образом, наиболее качественные принтеры изготавливает фирма
Hewlett Packard, немного им уступают принтеры фирм Canon и Epson. Наименее качественными являются принтеры фирм Oki (качество не превышает 20%
от качества принтеров Hewlett Packard)

и Lexmark, качество которых не выше 26% от качества принтеров Hewlett Packard.

Обратите внимание, что расчет по всем методам дает приблизительно
одинаковую оценку коэффициентов относительной важности.