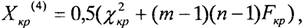Проверка согласованности мнений экспертов
Согласованность экспертов при ранжировании объектов оценивается коэффициентом конкордации (согласия)
(4)
Здесь Коэффициент К0 равен единице, когда все эксперты одинаково проранжировали объекты, и равен нулю при одинаковых суммах рангов всех объектов. Разработаны приемы проверки значимости коэффициента конкордации, В этом случае надо заменить группу экспертов или вывести из ее состава В качестве статистики X используют одну из двух:
(5)
(6) 1) для малых значений n и m используется статистика X (¹). Ее критические значения при следующих сочетаниях n и m приведены в приложении 7 [9], а также в приложении 1 данного пособия: n = 3 m = 2 - 15; n = 4 m = 2 - 8; n = 5 m = 2 - 8; n = 6 m = 2 - 8; n = 7 m = 7 - 8; 2) при n ≥ 20 и m ≥ 13 также следует использовать статистику X(¹), которая имеет при этих условиях χ² - распределение Пирсона с числом степеней свободы v= n - 1; 3) при 7 ≤ n ≤ 19 и m ≥ 13 следует использовать статистику X (²), распределение которой при этих условиях хорошо аппроксимируется F -распределением Фишера с числами степеней свободы v1 = n - 1 и v2 = (m - l)(n - l); 4) при n ≥ 8 и 7 ≤ m ≤ 12 следует использовать статистику X (²), распределение которой при этих условиях также хорошо аппроксимируется F -распределением Фишера с числами степеней свободы v1 = n - 1 и
5) при n ≤ 7 и m ≥ 8 (кроме случаев п. 1 и п. 3) используют составную статистику
где χ²кр - критическое значение χ² - распределения при числе степеней свободы v = n - 1; F кр - критическое значение F -распределения при числе степеней свободы v1 = n - 1 и v2 = (m - 1)(n - 1);
6) при n ≥ 8 и m = 3 - 6, а также при n = 7 и m = 2 - 6 используют статистику:
которую сравнивают с величиной
где χ²кр и Fкр определены так же, как в п. 5.
|

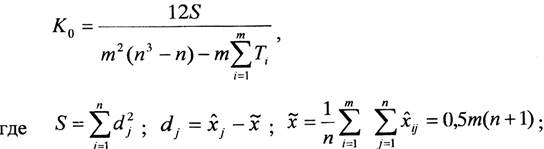

 - сумма нормализованных рангов, данных всеми экспертами j -му объекту;
- сумма нормализованных рангов, данных всеми экспертами j -му объекту;  - среднее значение сумм рангов по всем объектам; dj - отклонение суммы рангов j -го объекта от среднего значения; tμi, - число повторений μ -го ранга в ранжировке i-го эксперта (длина μ -ой группы).
- среднее значение сумм рангов по всем объектам; dj - отклонение суммы рангов j -го объекта от среднего значения; tμi, - число повторений μ -го ранга в ранжировке i-го эксперта (длина μ -ой группы).
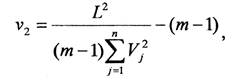 (7)
(7)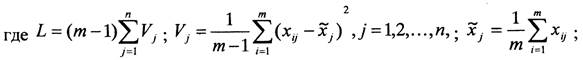
 (8)
(8)
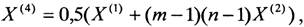 (9)
(9)