Данный метод базируется на формировании матрицы предпочтений [1,3].
Элемент aij матрицы предпочтений А определяет число случаев, когда эксперты
предпочитают (считают более важным) i -й объект j -му. Матрицу А нетрудно
построить, располагая ранжировками m экспертов, при этом для элементов
матрицы должно выполняться условие aji = m- aij. От матрицы предпочтений А
переходят к матрице вероятностей Р, разделив каждый элемент матрицы А на
m. Для элементов pij матрицы Р справедливо условие pij+pji=1.
Значения 0 и 1 в матрице Р заменяются соответственно на  и
и 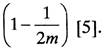
Дальнейшие преобразования основаны на следующей модели экспертных
оценок (модель Тэрстоуна). Полагается, что каждый объект обладает некоторой
«истинной» важностью zi, а оценки экспертов важности i-го объекта распределены нормально с математическим ожиданием zi,
и одной и той же дисперсией σ², характеризующей масштаб измерения величины zi. Положим σ²=1. При такой модели вероятность предпочтения экспертами i-го объекта j-му находится как Ф (zi -zj), где  - функция нормированного нормального распределения.
- функция нормированного нормального распределения.
Используя pij в качестве оценок для Ф (zi -zj), найдем с помощью таблиц
нормированного нормального распределения оценки zij = zi – zj:
 (14)
(14)
где  — функция, обратная Ф.
— функция, обратная Ф.
Теперь, располагая значениями 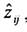 можно найти
можно найти  :
:
 (15)
(15)
В качестве оценок относительной важности используются величины
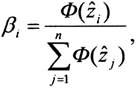 (16)
(16)
где Ф(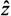 ij) - функция нормированного нормального распределения.
ij) - функция нормированного нормального распределения.
3.2. Парные сравнения

 и
и 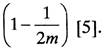
 - функция нормированного нормального распределения.
- функция нормированного нормального распределения. (14)
(14) — функция, обратная Ф.
— функция, обратная Ф.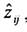 можно найти
можно найти  :
: (15)
(15)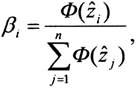 (16)
(16)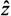 ij) - функция нормированного нормального распределения.
ij) - функция нормированного нормального распределения.


