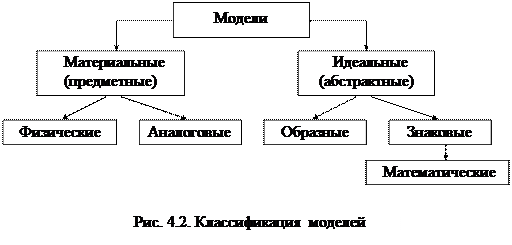
Классификация моделей

Существующее многообразие всевозможных моделей можно условно разделить на два класса: материальные (предметные) и идеальные (абстрактные) модели (рис.4.2).

Основными видами материальных моделей являются физические и аналоговые модели, а основными видами идеальных моделей – образные и знаковые. Математические модели принадлежат к разновидности знаковых моделей. Возможны и другие виды моделей (образно-знаковые, звуковые, лингвистические и др.). Отметим, что изучение материальных объектов носит экспериментальный характер, а изучение абстрактных моделей – теоретический.

Физическая модель – установка, устройство или приспособление, позволяющие проводить исследование подобного им реального объекта (натуры) экспериментальным путем с последующим перенесением результатов с модели на натуру на основе теории подобия.

 

 

Физическое моделирование применяется при исследовании сложных систем (объектов, явлений), функционирование которых либо не поддается адекватному математическому описанию, либо реализуется проще и с меньшими затратами на физических моделях, чем на математических. Часто физическое моделирование оказывается предпочтительнее математического, поскольку позволяет естественным образом учесть многие реальные особенности процессов в объекте и в силу этого полнее отразить физическую сущность явления. Поэтому физические модели применяют для проверки и отработки математических моделей, расчетных методов и общего решения сложных задач. Однако физическое моделирование с целью оптимизации свойств объектов требует больших затрат средств и времени и значительно уступает математическому моделированию по объему получаемой информации. В силу этого физические модели часто используют для того, чтобы подтвердить расчет по принятой математической модели. Доработанный метод расчета затем уверенно применяют для проектирования, оптимизации, оценки функционирования реального объекта и ему подобных объектов.

Физические модели широко применяются в электро- и теплоэнергетике, в гидро- и аэродинамике, в строительстве, кораблестроении, машиностроении и других отраслях науки и техники. Это модели мостов, плотин, телерадиобашен, сейсмостойких сооружений, кораблей, танкеров, атомных реакторов, турбин, самолетов, ракет, автомобилей и др.

Аналоговая модель – объект, имеющий физическую природу, отличную от природы оригинала, но замещающий оригинал на том основании, что оба объекта: оригинал и модель описываются аналогичными по форме уравнениями. Это позволяет переносить информацию об одном объекте (модели) на другой (оригинал).

Так, например, известны аналогии между электрическими, гидродинамическими, тепловыми, механическими и другими явлениями. Общность их математического описания позволяет на основании изучения свойств одного явления делать заключения о свойствах другого, менее изученного явления.

Математическая модель – система математических соотношений, приближенно описывающих изучаемый процесс или явление.

Таковыми служат все известные математические выражения законов физики: Гука - в теории упругости, Фурье - в теории теплопроводности, Навье-Стокса – в гидродинамике и др.

Экономико-математическая модель – математическое описание исследуемого экономического процесса, явления или объекта.

Эта модель описывает закономерности экономического процесса в абстрактном виде с помощью математических соотношений. Такими моделями являются модели, используемые для решения задач распределения ресурсов, управления запасами, организации рациональных перевозок товаров, планирования капиталовложений и др.

Нас с вами, в первую очередь, будут интересовать такие экономико-математические модели, которые можно было бы эффективно применять на практике в менеджменте организации, т.е. такие модели, которые:

q адекватно описывали бы управленческую ситуацию;

q позволяли бы определять основные тенденции ее развития;

q проводить анализ ее устойчивости и чувствительности к изменениям;

q выявлять ожидаемые опасности и возможные перспективы;

q отыскивать оптимальное сочетание ожидаемого эффекта и затрачиваемых ресурсов.

К классу таких моделей можно отнести модели исследования операций и имитационные модели.