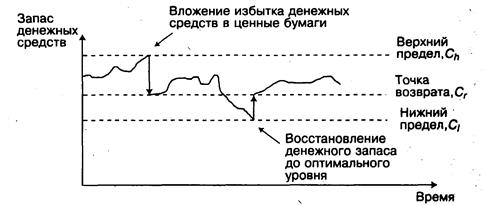
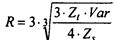Модель Миллера-Орра

Модель Баумоля проста и в достаточной степени приемлема для предприятий, денежные расходы которых стабильны и прогнозируе­мы. В действительности такое случается редко — остаток средств на расчетном счете изменяется случайным образом, причем возможны значительные колебания.

Модель, разработанная Миллером и Орром, представляет собой компромисс между простотой и повседневной реальностью. Она по­могает ответить на вопрос: как предприятию следует управлять де­нежным запасом, если невозможно предсказать каждодневный отток или приток денежных средств. Миллер и Орр использовали при пост­роении модели процесс Бернулли — стохастический процесс, в кото­ром поступление и расходование денег от периода к периоду являют­ся независимыми случайными событиями.

Логика действий финансового менеджера по управлению остат­ком средств на расчетном счете представлена на рис. 11.9 и заключа­ется в следующем. Остаток средств на счете хаотически меняется до тех пор, пока не достигает верхнего предела. Как только это происхо­дит, предприятие начинает скупать достаточное количество ликвидных ценных бумаг с целью вернуть запас денежных средств к некото­рому нормальному уровню (точке возврата). Если запас денежных средств достигает нижнего предела, то в этом случае предприятие продает накопленные ранее ценные бумаги и таким образом пополня­ет запас денежных средств до нормального предела.

Рис. 11.9. Модель Миллера-Орра

При решении вопроса о размахе вариации (разность между верх­ним и нижним пределами) рекомендуется придерживаться следующей политики: если ежедневная изменчивость денежных потоков велика или постоянные затраты, связанные с покупкой и продажей ценных бумаг высоки, то предприятию следует увеличить размах вариации и наоборот. Также рекомендуется уменьшить размах вариации, если есть возможность получения дохода благодаря высокой процентной став­ке по ценным бумагам.

Реализация модели осуществляется в несколько этапов:

1. Устанавливается минимальная величина денежных средств (С₁), которую целесообразно постоянно иметь на расчетном счете (опреде­ляется экспертным путем исходя из средней потребности предприя­тия в оплате счетов, возможных требований банка, кредиторов и др.).

2. По статистическим данным определяется вариация ежедневно­го поступления средств на расчетный счет (Var).

3. Определяются расходы (Zs) по хранению средств на расчетном счете (обычно их принимают в сумме ставки ежедневного дохода по краткосрочным ценным бумагам, циркулирующим на рынке) и расхо­ды (Zt) по взаимной трансформации денежных средств и ценных бу­маг (эта величина предполагается постоянной; аналогом такого вида расходов, имеющим место в отечественной практике, являются, на­пример, комиссионные, уплачиваемые в пунктах обмена валюты).

4. Рассчитывают размах вариации остатка денежных средств на расчетном счете (К) по формуле

5. Рассчитывают верхнюю границу денежных средств на расчет­ном счете (Cfi), при превышении которой необходимо часть денежных средств конвертировать в краткосрочные ценные бумаги:

Ch=Ci+R.

6. Определяют точку возврата (Cr) — величину остатка денежных средств на расчетном счете, к которой необходимо вернуться в слу­чае, если фактический остаток средств на расчетном счете выходит за границы интервала (Сi, Сh,):

Пример

Приведены следующие данные, необходимые для оптимизации остатка денежных средств компании:

минимальный запас денежных средств (Сi) — 10 тыс. долл.;

расходы по конвертации ценных бумаг (Zt) — 25 долл.;

процентная ставка r = 11,6% в год;

среднее квадратическое отклонение в день — 2000 долл.

С помощью модели Миллера-Орра определить политику управле­ния средствами на расчетном счете. -

Решение

1. Расчет показателя Z,:

(l+Zs)³⁶⁵=1.116

отсюда: Zs = 0,0003, или 0,03% в день.

2. Расчет вариации ежедневного денежного потока;

Var = 2000² = 4 000 000.

3. Расчет размаха вариации (R):

4. Расчет верхней границы денежных средств и точки возврата:

Сh = 10000 + 18900 = 28900 долл.

Cr = 10000 + 1/3 • 18900 = 16300 долл.

Таким образом, остаток средств на расчетном счете должен варь­ировать в интервале (10000, 28900); при выходе за его пределы не­обходимо восстановить средства на расчетном счете — 16300 долл. Западными специалистами разработаны и другие, более изощрен­ные подходы к управлению целевым остатком денежных средств; в ча­стности, определенную известность получили модель Стоуна, представ­ляющая собой развитие модели Миллера-Орра и имитационное моде­лирование по методу Монте-Карло [Бригхем, Гапенски, т.2, с. 313—316].