Теоретичні відомості. (теорію до даної роботи див
(теорію до даної роботи див. також у конспекті лекцій, §§5.1-5.3)
де g – прискорення вільного падіння, L – зведена довжина фізичного маятника,
I – момент інерції маятника відносно осі обертання, що проходить через точку О, m – маса маятника, l – віддаль від осі обертання до центра мас. Точка К, що лежить на лінії ОС і віддалена від точки О на зведену довжину L маятника, називається центром коливань. Якщо такий маятник буде здійснювати коливання відносно осі, що проходить через точку К, то період коливань буде рівний періоду коливань відносно осі, що проходить через точку O. Тому точки К і О називають спряженими. Маятник, котрий може коливатися відносно двох спряжених точок, називається оборотним. Покажемо, що періоди коливань відносно осей, що проходять через точки К і О, однакові. Позначимо зведену довжину фізичного маятника при коливаннях відносно осі, що проходить через точку К, через Зведені довжини при коливаннях маятника відносно осей, що проходять через точки К і О,
де
( З (2) і (3) одержимо
З рис. 1 видно, що
Враховуючи перше з рівнянь (4), з (6) одержимо Практично підібрати такі точки О і К, відносно яких періоди коливань маятника були б однакові, важко. Оскільки періоди коливань дещо відрізняються, то згідно з формулами (1), (3) та (4) маємо
Виключаючи з рівнянь (7)
Якщо маятник оборотний, тобто
Остання формула використовується для визначення прискорення вільного падіння.
|

 Оборотний маятник – частковий випадок фізичного маятника. Фізичним маятником називається будь-яке тверде тіло, котре може коливатися у полі тяжіння навколо горизонтальної осі, що не проходить через його центр мас. Точка перетину О осі з вертикальною площиною, що проходить через центр мас С маятника називається точкою підвісу. При рівноважному положенні маятника точки О і С знаходяться на одній вертикалі, причому центр мас розміщений нижче точки підвісу (рис. 1). Якщо відхилити маятник на невеликий кут і відпустити його, то він буде здійснювати гармонічні коливання з періодом
Оборотний маятник – частковий випадок фізичного маятника. Фізичним маятником називається будь-яке тверде тіло, котре може коливатися у полі тяжіння навколо горизонтальної осі, що не проходить через його центр мас. Точка перетину О осі з вертикальною площиною, що проходить через центр мас С маятника називається точкою підвісу. При рівноважному положенні маятника точки О і С знаходяться на одній вертикалі, причому центр мас розміщений нижче точки підвісу (рис. 1). Якщо відхилити маятник на невеликий кут і відпустити його, то він буде здійснювати гармонічні коливання з періодом , (1)
, (1)
 . (2)
. (2) . Якщо доведемо, що
. Якщо доведемо, що  , то цим згідно з формулою (1) буде доведено, що періоди коливань відносно осей, котрі проходять через точки К і О, однакові.
, то цим згідно з формулою (1) буде доведено, що періоди коливань відносно осей, котрі проходять через точки К і О, однакові. , (3)
, (3) і
і  – моменти інерції маятника відносно відповідних осей. За теоремою Штейнера
– моменти інерції маятника відносно відповідних осей. За теоремою Штейнера (4)
(4) – момент інерції маятника відносно осі, що проходить через центр мас).
– момент інерції маятника відносно осі, що проходить через центр мас). . (5)
. (5)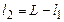 . Підставляючи це співвідношення у (5), одержимо
. Підставляючи це співвідношення у (5), одержимо . (6)
. (6) , що і потрібно було довести.
, що і потрібно було довести. . (7)
. (7) , знайдемо
, знайдемо . (8)
. (8) , то з (3) одержимо
, то з (3) одержимо . (9)
. (9)


