(теорію до даної роботи див. також у конспекті лекцій, §§4.2-4.3)

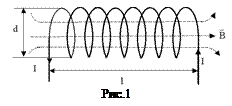 1. Соленоїд є системою послідовно з’єднаних однакових колових струмів (рис.1), тому для розрахунку індукції В магнітного поля в довільній точці на осі соленоїда потрібно спочатку розглянути магнітне поле на осі колового струму (одного витка соленоїда) (рис.2). Виберемо елемент струму
1. Соленоїд є системою послідовно з’єднаних однакових колових струмів (рис.1), тому для розрахунку індукції В магнітного поля в довільній точці на осі соленоїда потрібно спочатку розглянути магнітне поле на осі колового струму (одного витка соленоїда) (рис.2). Виберемо елемент струму  . Вектор індукції магнітного поля, породженого цим елементом в точці А, положення котрої задається радіус-вектором
. Вектор індукції магнітного поля, породженого цим елементом в точці А, положення котрої задається радіус-вектором  , визначається законом Біо-Савара-Лапласа (у вакуумі)
, визначається законом Біо-Савара-Лапласа (у вакуумі)
 , (1)
, (1)
де  – магнітна стала. При цьому
– магнітна стала. При цьому  можна розкласти на дві складові:
можна розкласти на дві складові:  – паралельну до осі Z і
– паралельну до осі Z і  – перпендикулярну до цієї осі. За принципом суперпозиції вектор індукції магнітного поля, створеного коловим струмом, тобто усіма елементами струму,
– перпендикулярну до цієї осі. За принципом суперпозиції вектор індукції магнітного поля, створеного коловим струмом, тобто усіма елементами струму,
 . (2)
. (2)
Тут враховано, що для усякого елементу  знайдеться симетричний елемент, що дає складову
знайдеться симетричний елемент, що дає складову  протилежного напрямку. Якщо врахувати, що
протилежного напрямку. Якщо врахувати, що  усіх елементів напрямлені вздовж осі Z, а також, що
усіх елементів напрямлені вздовж осі Z, а також, що 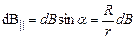 і
і  , то після підстановки (1) у (2) отримаємо для індукції магнітного поля на осі колового струму
, то після підстановки (1) у (2) отримаємо для індукції магнітного поля на осі колового струму
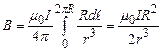 . (3)
. (3)
Зауважимо, що в центрі колового струму ( )
)
 .
.
 2. Для розрахунку індукції магнітного поля соленоїда розглянемо його осьовий переріз (рис.3),припускаючи постійність щільності намотки вздовж осі Z. Якщо на одиницю довжини соленоїда припадає n витків, то на ділянці довжиною dz буде ndz витків, які в точці А створять магнітне поле з індукцією
2. Для розрахунку індукції магнітного поля соленоїда розглянемо його осьовий переріз (рис.3),припускаючи постійність щільності намотки вздовж осі Z. Якщо на одиницю довжини соленоїда припадає n витків, то на ділянці довжиною dz буде ndz витків, які в точці А створять магнітне поле з індукцією
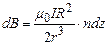 . (4)
. (4)
Врахувавши, що 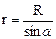 ,
, 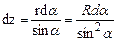 , після інтегрування (4) по всій довжині соленоїда отримаємо для індукції магнітного поля на осі соленоїда
, після інтегрування (4) по всій довжині соленоїда отримаємо для індукції магнітного поля на осі соленоїда
 . (5)
. (5)
Якщо соленоїд дуже довгий 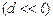 , то
, то 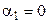 і
і  . Тоді
. Тоді
 . (6)
. (6)
Зауважимо, що формулу (6) можна отримати, використавши теорему про циркуляцію вектора індукції магнітного поля. Для дуже довгого соленоїда магнітне поле практично однорідне (силові лінії еквідистантні і паралельні до осі соленоїда). Для реальних соленоїдів, коли нерівність 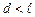 слабка, поле найсильніше в центрі соленоїда і зменшується при наближенні до його кінців.
слабка, поле найсильніше в центрі соленоїда і зменшується при наближенні до його кінців.
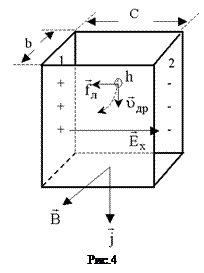 3. Для визначення індукції магнітного поля на осі соленоїда в цій роботі використовуються напівпровідникові датчики, дія яких грунтується на ефекті Холла,–датчики Холла (ДХ) (рис.4). Нехай для ДХ використано напівпровідниковий кристал з дірковою провідністю (носії струму – дірки (hole)). Якщо вздовж такого кристалу протікає електричний струм з густиною
3. Для визначення індукції магнітного поля на осі соленоїда в цій роботі використовуються напівпровідникові датчики, дія яких грунтується на ефекті Холла,–датчики Холла (ДХ) (рис.4). Нехай для ДХ використано напівпровідниковий кристал з дірковою провідністю (носії струму – дірки (hole)). Якщо вздовж такого кристалу протікає електричний струм з густиною  і він розміщений в поперечному магнітному полі з індукцією
і він розміщений в поперечному магнітному полі з індукцією 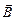 , то на носії струму, заряд яких е, і які рухаються з дрейфовою швидкістю
, то на носії струму, заряд яких е, і які рухаються з дрейфовою швидкістю  , буде діяти сила Лоренца
, буде діяти сила Лоренца
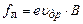 . (7)
. (7)
Ця сила, як видно з рис.4, буде відхиляти носії до грані 1, і між гранями 1 та 2 виникне поперечне холлівське поле з напруженістю  , значення якої визначене з умови рівноваги
, значення якої визначене з умови рівноваги 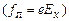 становить
становить
 . (8)
. (8)
Різниця потенціалів між гранями 1, 2 або холлівська напруга складає
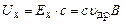 . (9)
. (9)
Якщо врахувати, що густина струму пов’язана з 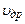 і концентрацією носіїв Р співвідношенням
і концентрацією носіїв Р співвідношенням  , то (9) перепишеться як
, то (9) перепишеться як
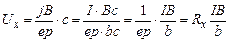 , (10)
, (10)
де І – сила струму через кристал, а  – постійна Холла.
– постійна Холла.
 Оскільки значення
Оскільки значення 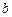 i
i 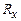 є фіксованими параметрами ДХ, а сила струму через кристал підтримується постійною (для ДХ цієї роботи
є фіксованими параметрами ДХ, а сила струму через кристал підтримується постійною (для ДХ цієї роботи 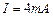 ), то доцільно ввести коефіцієнт пропорційності
), то доцільно ввести коефіцієнт пропорційності 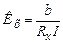 , і тоді (10) запишеться як
, і тоді (10) запишеться як
 . (11)
. (11)
Отже, для визначення значення індукції магнітного поля соленоїда достатньо виміряти холлівську напругу між контактами 1–2 ДХ (рис.5) і помножити її на 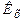 . Ситуація дещо ускладнюється можливою нееквіпотенціальністю контактів 1, 2, що приво-дить до появи напруги нееквіпотенціальностї
. Ситуація дещо ускладнюється можливою нееквіпотенціальністю контактів 1, 2, що приво-дить до появи напруги нееквіпотенціальностї 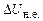 навіть при відсутності магнітного поля. В цьому випадку
навіть при відсутності магнітного поля. В цьому випадку
 (12)
(12)
де  – напруга, що вимірюється вольтметром з великим вхідним опором (чи потенціометром), приєднаним безпосередньо до контактів 1, 2 ДХ. Параметри
– напруга, що вимірюється вольтметром з великим вхідним опором (чи потенціометром), приєднаним безпосередньо до контактів 1, 2 ДХ. Параметри 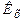 і
і 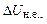 а також кількість витків
а також кількість витків  , довжина
, довжина 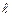 і діаметр
і діаметр  соленоїда задаються як паспортні дані блоку соленоїда.
соленоїда задаються як паспортні дані блоку соленоїда.
4. Блок-схема експериментальної установки показана на рис.6.
Блок живлення забезпечує регульований (регулятор Р) струм через соленоїд  який вимірюється амперметром А, а також струм ДХ (І=4mA). Датчик Холла розміщений на рухомому штоці з міліметровою шкалою, нульова позначка якої фіксує положення ДХ в центрі соленоїда. Напруга на зондових контактах датчика Холла вимірюється цифровим вольтметром з точністю до третього знаку після коми.
який вимірюється амперметром А, а також струм ДХ (І=4mA). Датчик Холла розміщений на рухомому штоці з міліметровою шкалою, нульова позначка якої фіксує положення ДХ в центрі соленоїда. Напруга на зондових контактах датчика Холла вимірюється цифровим вольтметром з точністю до третього знаку після коми.


 1. Соленоїд є системою послідовно з’єднаних однакових колових струмів (рис.1), тому для розрахунку індукції В магнітного поля в довільній точці на осі соленоїда потрібно спочатку розглянути магнітне поле на осі колового струму (одного витка соленоїда) (рис.2). Виберемо елемент струму
1. Соленоїд є системою послідовно з’єднаних однакових колових струмів (рис.1), тому для розрахунку індукції В магнітного поля в довільній точці на осі соленоїда потрібно спочатку розглянути магнітне поле на осі колового струму (одного витка соленоїда) (рис.2). Виберемо елемент струму  . Вектор індукції магнітного поля, породженого цим елементом в точці А, положення котрої задається радіус-вектором
. Вектор індукції магнітного поля, породженого цим елементом в точці А, положення котрої задається радіус-вектором  , визначається законом Біо-Савара-Лапласа (у вакуумі)
, визначається законом Біо-Савара-Лапласа (у вакуумі) , (1)
, (1) – магнітна стала. При цьому
– магнітна стала. При цьому  можна розкласти на дві складові:
можна розкласти на дві складові:  – паралельну до осі Z і
– паралельну до осі Z і  – перпендикулярну до цієї осі. За принципом суперпозиції вектор індукції магнітного поля, створеного коловим струмом, тобто усіма елементами струму,
– перпендикулярну до цієї осі. За принципом суперпозиції вектор індукції магнітного поля, створеного коловим струмом, тобто усіма елементами струму, . (2)
. (2)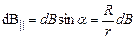 і
і  , то після підстановки (1) у (2) отримаємо для індукції магнітного поля на осі колового струму
, то після підстановки (1) у (2) отримаємо для індукції магнітного поля на осі колового струму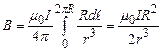 . (3)
. (3) )
) .
. 2. Для розрахунку індукції магнітного поля соленоїда розглянемо його осьовий переріз (рис.3),припускаючи постійність щільності намотки вздовж осі Z. Якщо на одиницю довжини соленоїда припадає n витків, то на ділянці довжиною dz буде ndz витків, які в точці А створять магнітне поле з індукцією
2. Для розрахунку індукції магнітного поля соленоїда розглянемо його осьовий переріз (рис.3),припускаючи постійність щільності намотки вздовж осі Z. Якщо на одиницю довжини соленоїда припадає n витків, то на ділянці довжиною dz буде ndz витків, які в точці А створять магнітне поле з індукцією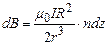 . (4)
. (4)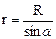 ,
, 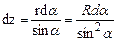 , після інтегрування (4) по всій довжині соленоїда отримаємо для індукції магнітного поля на осі соленоїда
, після інтегрування (4) по всій довжині соленоїда отримаємо для індукції магнітного поля на осі соленоїда . (5)
. (5)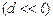 , то
, то 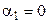 і
і  . Тоді
. Тоді . (6)
. (6)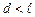 слабка, поле найсильніше в центрі соленоїда і зменшується при наближенні до його кінців.
слабка, поле найсильніше в центрі соленоїда і зменшується при наближенні до його кінців. 3. Для визначення індукції магнітного поля на осі соленоїда в цій роботі використовуються напівпровідникові датчики, дія яких грунтується на ефекті Холла,–датчики Холла (ДХ) (рис.4). Нехай для ДХ використано напівпровідниковий кристал з дірковою провідністю (носії струму – дірки (hole)). Якщо вздовж такого кристалу протікає електричний струм з густиною
3. Для визначення індукції магнітного поля на осі соленоїда в цій роботі використовуються напівпровідникові датчики, дія яких грунтується на ефекті Холла,–датчики Холла (ДХ) (рис.4). Нехай для ДХ використано напівпровідниковий кристал з дірковою провідністю (носії струму – дірки (hole)). Якщо вздовж такого кристалу протікає електричний струм з густиною  і він розміщений в поперечному магнітному полі з індукцією
і він розміщений в поперечному магнітному полі з індукцією 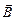 , то на носії струму, заряд яких е, і які рухаються з дрейфовою швидкістю
, то на носії струму, заряд яких е, і які рухаються з дрейфовою швидкістю  , буде діяти сила Лоренца
, буде діяти сила Лоренца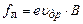 . (7)
. (7) , значення якої визначене з умови рівноваги
, значення якої визначене з умови рівноваги 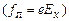 становить
становить . (8)
. (8)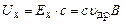 . (9)
. (9)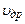 і концентрацією носіїв Р співвідношенням
і концентрацією носіїв Р співвідношенням  , то (9) перепишеться як
, то (9) перепишеться як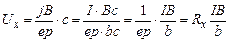 , (10)
, (10) – постійна Холла.
– постійна Холла. Оскільки значення
Оскільки значення 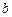 i
i 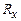 є фіксованими параметрами ДХ, а сила струму через кристал підтримується постійною (для ДХ цієї роботи
є фіксованими параметрами ДХ, а сила струму через кристал підтримується постійною (для ДХ цієї роботи 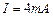 ), то доцільно ввести коефіцієнт пропорційності
), то доцільно ввести коефіцієнт пропорційності 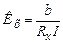 , і тоді (10) запишеться як
, і тоді (10) запишеться як . (11)
. (11)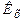 . Ситуація дещо ускладнюється можливою нееквіпотенціальністю контактів 1, 2, що приво-дить до появи напруги нееквіпотенціальностї
. Ситуація дещо ускладнюється можливою нееквіпотенціальністю контактів 1, 2, що приво-дить до появи напруги нееквіпотенціальностї 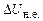 навіть при відсутності магнітного поля. В цьому випадку
навіть при відсутності магнітного поля. В цьому випадку (12)
(12) – напруга, що вимірюється вольтметром з великим вхідним опором (чи потенціометром), приєднаним безпосередньо до контактів 1, 2 ДХ. Параметри
– напруга, що вимірюється вольтметром з великим вхідним опором (чи потенціометром), приєднаним безпосередньо до контактів 1, 2 ДХ. Параметри 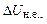 а також кількість витків
а також кількість витків  , довжина
, довжина 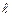 і діаметр
і діаметр  соленоїда задаються як паспортні дані блоку соленоїда.
соленоїда задаються як паспортні дані блоку соленоїда. який вимірюється амперметром А, а також струм ДХ (І=4mA). Датчик Холла розміщений на рухомому штоці з міліметровою шкалою, нульова позначка якої фіксує положення ДХ в центрі соленоїда. Напруга на зондових контактах датчика Холла вимірюється цифровим вольтметром з точністю до третього знаку після коми.
який вимірюється амперметром А, а також струм ДХ (І=4mA). Датчик Холла розміщений на рухомому штоці з міліметровою шкалою, нульова позначка якої фіксує положення ДХ в центрі соленоїда. Напруга на зондових контактах датчика Холла вимірюється цифровим вольтметром з точністю до третього знаку після коми.


