(теорію до даної роботи див. також у конспекті лекцій, §§4.1, 4.4, 5.1, 5.3)
Нехай у магнітному полі з індукцією 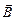 знаходиться лінійний елемент струму
знаходиться лінійний елемент струму  . На нього з боку поля діє сила, величина і напрямок котрої визначаються законом Ампера
. На нього з боку поля діє сила, величина і напрямок котрої визначаються законом Ампера
 , (1)
, (1)
або у скалярній формі
 , (2)
, (2)
де  – кут між
– кут між 
 та
та 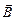 .
.
Сила, що діє на провідник зі струмом скінченої довжини, знаходиться з (1) або (2) інтегруванням по всій довжині провідника  . (3)Зокрема, для прямолінійного провідника в однорідному магнітному полі
. (3)Зокрема, для прямолінійного провідника в однорідному магнітному полі  з (3) одержимо
з (3) одержимо
 . (4)
. (4)
Напрямок сили Ампера знаходиться за правилом лівої руки (рис.2).
Щоб одержати формулу для обчислення сили Ампера в даній лабораторній роботі, розглянемо рівняння руху фізичного маятника (рамки abcd) Цей маятник здійснює коливання відносно осі cd. Застосуємо до нього основний закон динаміки обертального руху твердого тіла
 , (5)
, (5)
де  – момент інерції маятника відносно осі cd,
– момент інерції маятника відносно осі cd,  –кутове прискорення,
–кутове прискорення,  – головний момент зовнішніх сил відносно цієї осі.
– головний момент зовнішніх сил відносно цієї осі.
 У відсутності струму обертовий момент створює сила тяжіння (прикладена до центра мас маятника).
У відсутності струму обертовий момент створює сила тяжіння (прикладена до центра мас маятника).
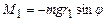 , (6)
, (6)
де 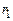 відстань від осі обертання до центра мас,
відстань від осі обертання до центра мас,  – кут відхилення маятника від положення рівноваги,
– кут відхилення маятника від положення рівноваги,  – маса маятника. Знак “–” показує, що момент сили тяжіння обертає маятник в бік, протилежний відхиленню від рівноваги.
– маса маятника. Знак “–” показує, що момент сили тяжіння обертає маятник в бік, протилежний відхиленню від рівноваги.
Якщо через провідник ab, що знаходиться в магнітному полі електромагніта М, проходить електричний струм, то на маятник, крім сили тяжіння, діє сила Ампера. Напрямок сили Ампера, в залежності від напрямку струму, або співпадає з напрямком сили тяжіння, або протилежний до нього. Сила Ампера прикладена до провідника ab і створює момент сили

 , (7)
, (7)
де 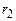 – відстань від провідника ab до осі обертання. Знак “–” в (7) відноситься до випадку, коли сила Ампера напрямлена вниз (рис.3), а знак “+” – коли вгору (рис.4).
– відстань від провідника ab до осі обертання. Знак “–” в (7) відноситься до випадку, коли сила Ампера напрямлена вниз (рис.3), а знак “+” – коли вгору (рис.4).
Після підстановки (7) і (6) в (5) одержимо
 .
.
Для малих кутів  , тому, якщо кут відхилення малий, останнє рівняння можна записати у вигляді
, тому, якщо кут відхилення малий, останнє рівняння можна записати у вигляді
 , або
, або  .
.
Введемо позначення
 , (8)
, (8)
тоді останнє рівняння набуде вигляду
 . (9)
. (9)
Вираз (9) – диференціальне рівняння вільних гармонічних коливань, розв’язок котрого

 , (10)
, (10)
де  – амплітудне значення кута відхилення,
– амплітудне значення кута відхилення,  – власна циклічна частота, квадрат якої визначається рівнянням (8). Якщо струм в провіднику ab відсутній, то
– власна циклічна частота, квадрат якої визначається рівнянням (8). Якщо струм в провіднику ab відсутній, то  , і маятник коливається з циклічною частотою
, і маятник коливається з циклічною частотою  . З (8) тоді
. З (8) тоді
 . (11)
. (11)
З (8) і (11) знайдемо  , або
, або
 . (12)
. (12)
Циклічна чистота пов’язана з періодом коливань співвідношенням  . Врахувавши це, а також виразивши І з (11), запишемо рівняння (12) у вигляді
. Врахувавши це, а також виразивши І з (11), запишемо рівняння (12) у вигляді
 ,
,
де  і
і  – періоди коливань маятника у відсутності та при наявності струму, відповідно. Відношення
– періоди коливань маятника у відсутності та при наявності струму, відповідно. Відношення  можна замінити відношенням проміжків часу
можна замінити відношенням проміжків часу  , за які маятник здійснив однакову кількість коливань. Тоді останнє рівняння набуде вигляду
, за які маятник здійснив однакову кількість коливань. Тоді останнє рівняння набуде вигляду
 , (13)
, (13)
де  – постійна лабораторної установки, яка вказана в її паспорті. Таким чином, вимірявши
– постійна лабораторної установки, яка вказана в її паспорті. Таким чином, вимірявши  і
і  , за формулою (13) можна розрахувати силу Ампера для кількох значень сили струму і побудувати графік залежності
, за формулою (13) можна розрахувати силу Ампера для кількох значень сили струму і побудувати графік залежності  . Оскільки напрямок струму в провіднику ab перпендикулярний до ліній магнітної індукції (див. рис.1), то формула (4) для сили Ампера набуде вигляду
. Оскільки напрямок струму в провіднику ab перпендикулярний до ліній магнітної індукції (див. рис.1), то формула (4) для сили Ампера набуде вигляду
 , (14)
, (14)
де  – довжина провідника ab.
– довжина провідника ab.
В даній лабораторній роботі індукція магнітного поля В залишається незмінною, тому залежність 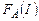 має бути пропорційною. В цьому суть перевірки закона Ампера. Визначивши
має бути пропорційною. В цьому суть перевірки закона Ампера. Визначивши  для даного значення сили струму, з (14) можна визначити індукцію магнітного поля
для даного значення сили струму, з (14) можна визначити індукцію магнітного поля
 . (15)
. (15)

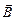 знаходиться лінійний елемент струму
знаходиться лінійний елемент струму  . На нього з боку поля діє сила, величина і напрямок котрої визначаються законом Ампера
. На нього з боку поля діє сила, величина і напрямок котрої визначаються законом Ампера , (1)
, (1) , (2)
, (2) – кут між
– кут між 
 та
та  . (3)Зокрема, для прямолінійного провідника в однорідному магнітному полі
. (3)Зокрема, для прямолінійного провідника в однорідному магнітному полі  з (3) одержимо
з (3) одержимо . (4)
. (4) , (5)
, (5) – момент інерції маятника відносно осі cd,
– момент інерції маятника відносно осі cd,  –кутове прискорення,
–кутове прискорення,  – головний момент зовнішніх сил відносно цієї осі.
– головний момент зовнішніх сил відносно цієї осі. У відсутності струму обертовий момент створює сила тяжіння (прикладена до центра мас маятника).
У відсутності струму обертовий момент створює сила тяжіння (прикладена до центра мас маятника).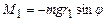 , (6)
, (6)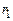 відстань від осі обертання до центра мас,
відстань від осі обертання до центра мас,  – кут відхилення маятника від положення рівноваги,
– кут відхилення маятника від положення рівноваги,  – маса маятника. Знак “–” показує, що момент сили тяжіння обертає маятник в бік, протилежний відхиленню від рівноваги.
– маса маятника. Знак “–” показує, що момент сили тяжіння обертає маятник в бік, протилежний відхиленню від рівноваги.
 , (7)
, (7)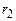 – відстань від провідника ab до осі обертання. Знак “–” в (7) відноситься до випадку, коли сила Ампера напрямлена вниз (рис.3), а знак “+” – коли вгору (рис.4).
– відстань від провідника ab до осі обертання. Знак “–” в (7) відноситься до випадку, коли сила Ампера напрямлена вниз (рис.3), а знак “+” – коли вгору (рис.4). .
. , тому, якщо кут відхилення малий, останнє рівняння можна записати у вигляді
, тому, якщо кут відхилення малий, останнє рівняння можна записати у вигляді , або
, або  .
. , (8)
, (8) . (9)
. (9) , (10)
, (10) – амплітудне значення кута відхилення,
– амплітудне значення кута відхилення,  – власна циклічна частота, квадрат якої визначається рівнянням (8). Якщо струм в провіднику ab відсутній, то
– власна циклічна частота, квадрат якої визначається рівнянням (8). Якщо струм в провіднику ab відсутній, то  , і маятник коливається з циклічною частотою
, і маятник коливається з циклічною частотою  . З (8) тоді
. З (8) тоді . (11)
. (11) , або
, або . (12)
. (12) . Врахувавши це, а також виразивши І з (11), запишемо рівняння (12) у вигляді
. Врахувавши це, а також виразивши І з (11), запишемо рівняння (12) у вигляді ,
, і
і  – періоди коливань маятника у відсутності та при наявності струму, відповідно. Відношення
– періоди коливань маятника у відсутності та при наявності струму, відповідно. Відношення  можна замінити відношенням проміжків часу
можна замінити відношенням проміжків часу  , за які маятник здійснив однакову кількість коливань. Тоді останнє рівняння набуде вигляду
, за які маятник здійснив однакову кількість коливань. Тоді останнє рівняння набуде вигляду , (13)
, (13) – постійна лабораторної установки, яка вказана в її паспорті. Таким чином, вимірявши
– постійна лабораторної установки, яка вказана в її паспорті. Таким чином, вимірявши  і
і  , за формулою (13) можна розрахувати силу Ампера для кількох значень сили струму і побудувати графік залежності
, за формулою (13) можна розрахувати силу Ампера для кількох значень сили струму і побудувати графік залежності  . Оскільки напрямок струму в провіднику ab перпендикулярний до ліній магнітної індукції (див. рис.1), то формула (4) для сили Ампера набуде вигляду
. Оскільки напрямок струму в провіднику ab перпендикулярний до ліній магнітної індукції (див. рис.1), то формула (4) для сили Ампера набуде вигляду , (14)
, (14) – довжина провідника ab.
– довжина провідника ab.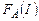 має бути пропорційною. В цьому суть перевірки закона Ампера. Визначивши
має бути пропорційною. В цьому суть перевірки закона Ампера. Визначивши  для даного значення сили струму, з (14) можна визначити індукцію магнітного поля
для даного значення сили струму, з (14) можна визначити індукцію магнітного поля . (15)
. (15)


