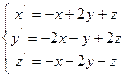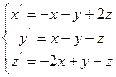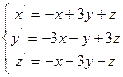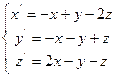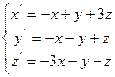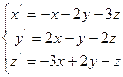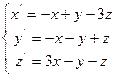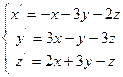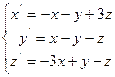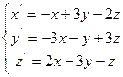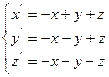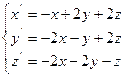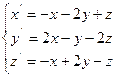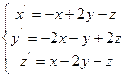Лабораторна робота № 2. Дослідження точки рівноваги на стійкість.

1. Перетворити числа між системами числення, вказаними у завданні. Детально розписати та пояснити процес перетворення.

2. Перетворити IP-адресу в двійкову систему числення.

3. Перетворити маску в двійкову систему числення.

4. Визначити мережево (вузлову) частину.

5. Пояснити розрахунки.

Варіанти індивідуальних завдань Таблиця 1

№ з/п	Число в системі числення з основою n	Перевести в систему числення з основою m	Знайти мережеву (вузлову) частину IP-адреси із заданою маскою підмережі
	10110, 111000, 100110, n = 2; АВ145, 4С35А, 9Е021, n = 16	m = 10	мережеву частину IP-адреси 192.168.25.13 з маскою 255.255.252.0
	110110, 10100, 101010, n = 2; 38А1В, А4С5А, 19DЕ42, n = 16	m = 10	мережеву частину IP-адреси 172.16.12.100 з маскою 255.254.0.0
	10010, 100101, 10101, n = 2; 2DА4В, F68СА, 25FDЕ, n = 16	m = 10	мережеву частину IP-адреси 10.13.50.3 з маскою 240.0.0.0
	11010, 101000, 1101010, n = 2; 7ВF3A, 22А5А, D4FA2, n = 16	m = 10	мережеву частину IP-адреси 196.170.30.12 з маскою 255.255.254.0
	101110, 11100, 101011, n = 2; А531В, СF5А9, BD362, n = 16	m = 10	мережеву частину IP-адреси 13.8.5.24 з маскою 254.0.0.0
	103, 245, 122, n = 10; F538В, 5А349, 362F5, n = 16	m = 2	мережеву частину IP-адреси 120.13.101.3 з маскою 255.240.0.0
	205, 144, 233, n = 10; АFВ22, 12345, 3А625, n = 16	m = 2	мережеву частину IP-адреси 100.100.100.20 з маскою 255.224.0.0
	186, 45, 217, n = 10; FВ333, А2139, 2F154, n = 16	m = 2	вузлову частину IP-адреси 11.13.15.18 з маскою 240.0.0.0
	218, 126, 174, n = 10; 2В412, 34С94, ВF222, n = 16	m = 2	вузлову частину IP-адреси 111.120.35.8 з маскою 255.254.0.0
	221, 195, 32, n = 10; F538В, 5А349, 362F5, n = 16	m = 2	вузлову частину IP-адреси 171.3.41.118 з маскою 255.252.0.0
	111000, 100101, 101100, n = 2; 234, 142, 211, n = 10	m = 16	вузлову частину IP-адреси 211.123.143.1 з маскою 255.255.192.0
	100011, 10101, 111100, n = 2; 215, 247, 123, n = 10	m = 16	вузлову частину IP-адреси 155.24.156.33 з маскою 255.240.0.0
	11000, 100110, 110011, n = 2; 255, 142, 188, n = 10	m = 16	вузлову частину IP-адреси 19.3.21.181 з маскою 240.0.0.0
	11000, 100110, 110011, n = 2; 201, 136, 111, n = 10	m = 16	вузлову частину IP-адреси 121.5.165.7 з маскою 255.252.0.0
	10101, 101100, 111110, n = 2; 222, 171, 184, n = 10	m = 16	вузлову частину IP-адреси 32.115.33.146 з маскою 252.0.0.0

Контрольні запитання

1. З чого складається система числення? Назвіть основні системи числення.

2. Які алгоритми перетворення чисел з десяткової системи числення у двійкову вам відомі?

3. Які основні правила перетворень шістнадцяткових чисел у двійкові (і навпаки)?

4. Як перетворити двійкове число в десяткове?

5. Як перетворити шістнадцяткове число в десяткове (і навпаки)?

6. Дайте визначення та склад IP-адреси.

7. Як представляється IP-адреса?

8. Для чого використовуються IP-адреси?

9. Що таке маска підмережі? Для чого вона використовується?

10. Як визначити мережеву частину IP-адреси?

 

Лабораторна робота № 2. Дослідження точки рівноваги на стійкість.

Мета: навчатися застосовувати критерії Рауса-Гурвіца і Л’єнара-Шипара.

 

Завдання: за даними Вашого варіанту:

1. Знайти координати точки рівноваги у MathCad:

а) методом оберненої матриці;

б) за допомогою функції lsolve;

в) за допомогою обчислювального блоку Given/Find.

2. Дослідити систему на стійкість двома критеріями: Рауса-Гурвіца і Л’єнара-Шипара. Результати порівняти. При застосуванні зазначених критеріїв використати функцію виділення підматриць (submatrix(A,ir,jr,ic,jc) – повертає підмасив, що складається зі всіх елементів, що містяться в рядках з ir по jr і стовпцях з ic по jc масиву A).

 

№ варіанта	Завдання	№ варіанта	Завдання

 

 

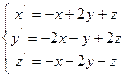
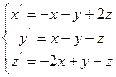
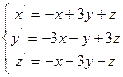
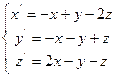
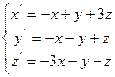
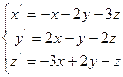
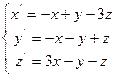
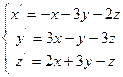
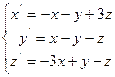
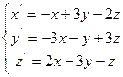
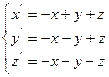
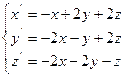
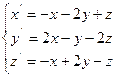
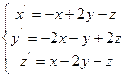
У звіті навести умову задачі, обчислення за кожним з методів (з поясненням використаних інструментів того ПЗ, який обрано Вами для обчислень), висновок. У висновку оцінити доцільність (зручність) використання кожного застосованого методу розв’язання систем лінійних рівнянь та кожного застосованого методу дослідження стійкості точки рівноваги.

 

Варіанти систем запозичено з