ЗАДАЧА № 3. Обработка результатов измерений
В процессе изготовления точных деталей для повышения точности определения их действительных размеров используют серию измерений одним и тем же измерительным средством в одних и тех же условиях. При этом возникает задача определения границы доверительного интервала изменения погрешности результатов измерений, абсолютной и относительной погрешности при некотором заданном уровне надежности (доверительной вероятности) определения результата измерения. Причем, возможны два случая: границы доверительного интервала изменения погрешности результатов измерений сравнимы по величине с величиной погрешности используемого измерительного средства, либо значительно меньше ее. Общий порядок обработки результатов измерений в подобных случаях: 1. Записать результаты измерений a i; 2. Вычислить среднее значение из n измерений а = 3. Определить погрешности отдельных измерений V i = а - а i; 4. Вычислить квадраты погрешностей отдельных измерений V i2; 5. Определить среднюю квадратическую погрешность результата серии измерений
6. Задаться значением надежности a (обычно выбирают одно из так называемых стандартных значений – 0,9; 0,95; 0,99; 0,995; 0,999); 7. Определить коэффициент Стьюдента t a(n) для выбранной надежности a и числа проведенных измерений n (см. табл. 3.1); 8. Найти границы доверительного интервала изменения погрешности результатов измерений D х = t a (n)× Sa Если эта величина окажется сравнимой с величиной d погрешности прибора, то в качестве границ доверительного интервала следует взять величину
9. Записать окончательный результат X = a ±D x; 10. Оценить относительную погрешность результата серии измерений e = Значения коэффициентов Стьюдента t a для различных значений надежности a и числа измерений n
Примеры 1. Микрометром было сделано 5 замеров диаметра цилиндра а i: 14,85; 14,80; 14,84; 14,81; 14,79. Цена деления микрометра 0,01 мм. Определить диаметр цилиндра с надежностью a = 0,95. Решение Для первых пяти измерений определим среднеарифметическое значение и границы доверительного интервала. Для удобства расчетов в качестве а о выберем произвольное число, удобное для расчетов: а о = 14,80 мм Определим разности (аi - а о) и квадраты этих разностей:
Найдем среднее значение а размера:
а - а о = 14,82 – 14,80 = 0, 02 мм; (а - а о)2 = 0, 022 = 0,0004 мм Найдем среднеквадратичное отклонение размеров Sа:
Для надежности a = 0,95 и n = 5 t a = 2,78. Абсолютная погрешность измерения D х: D х = t a× Sа = 2,78 × 0,0116 = 0,0322» 0,03 мм. Относительная погрешность измерения e а = Результат измерения можно представить в виде (14,82 - 0,03) мм £ а £ (14,82 + 0,03) мм, или а = (14,82 ± 0,03) мм.
2. Определить, сколько деталей из всей партии запуска N = 1220деталей следует подвергнуть повторному контролю в порядке случайной выборки, чтобы с вероятностью a = 0,95 предельная ошибка (абсолютная погрешность) не превышала 3% от среднего размера деталей x = 42 мм. Коэффициент вариации среднего размера по данным предыдущих проверок составляет V s = 6% = 0,06. Решение: Абсолютная погрешность измерения D Х = e× х = 0,03×42 = 1,26 мм. где e = 3% – установленная относительная погрешность измерения. Среднее квадратичное отклонение: SX = V s× x = 0,06×42 = 2,52 мм. Оптимальная численность выборки для повторного отбора: n = N × t a(N)2× SX 2/(D2 X × N + t 2× SX 2) = = 1220×22×2,522/(1,262×1220 + 22×2,522) = 15,8 где: t a(N) – коэффициент Стьюдента t a(n) для выбранного уровня надежности (вероятности) a и числа проведенных измерений n, в нашем случае количество деталей настолько велико, что приближенно можно считать, что оно близко к бесконечности (см. табл. 3.1): t a(N) = t a (1220)» t a (¥) = 1,96 Таким образом необходимо обследовать 16 деталей.
|

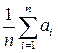
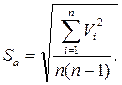
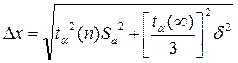 .
.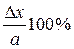 .
.
 , мм;
, мм;
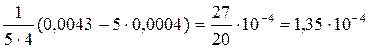 мм2
мм2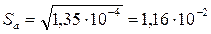 мм.
мм.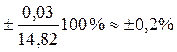 .
.


