ЗАДАЧА № 7. Размерные цепи
Важнейшей проблемой технологии машиностроения является обеспечение заданной точности изготовления изделий и их взаимозаменяемости. Основной теоретический аппарат обеспечения размерной точности и взаимозаменяемости сборочных единиц в машиностроении - теория размерных цепей. С помощью размерных цепей можно решать конструкторские, технологические, измерительные и прочие задачи. Расчет размерных цепей позволяет обоснованно назначать допуски на взаимосвязанные размеры деталей и сборочных единиц; облегчает правильную простановку размеров на чертежах, согласованную с порядком обработки деталей и сборки механизмов. Размерные цепи применяют для определения операционных допусков, пересчета конструкторских баз на технологические, для выбора измерительных баз, для решения ряда задач по оптимизации обработки и сборки изделий и т.д. Размерная цепь – совокупность размеров, образующих замкнутый контур и непосредственно участвующих в решении поставленной задачи. Звено размерной цепи – один из размеров, образующих размерную цепь. Звенья, образующие размерную цепь, обозначают любой общей буквой, принятой для данной размерной цепи, с порядковыми цифровыми индексами: A1, А2, A3... и т.п., замыкающее звено обозначают либо как A0, либо Х, У и т.п.
Виды звеньев размерных цепей Замыкающее звено А0— звено размерной цепи, которое получается последним в процессе изготовления или сборки. Исходное звено А0 — звено, получающееся по условию задачи, для решения которой используется размерная цепь. Чаще всего замыкающее или исходное – это звено, точность которого определяет работоспособность механизма, а следовательно, и составляющих звеньев. В качестве замыкающих и исходных звеньев используют детали (например, комплект прокладок), зазоры, натяги и т.д. Поэтому, числовые значения указанных звеньев могут быть положительными, отрицательными и равными нулю. Составляющее звено Аk — звено, изменение которого вызывает изменение замыкающего звена. Составляющие звенья могут быть увеличивающими и уменьшающими. Увеличивающее звено — звено, с увеличением которого увеличивается замыкающее (исходное) звено. Их принято обозначать в виде Уменьшающее звено — звено, с увеличением которого уменьшается замыкающее (исходное) звено. Их принято обозначать в виде
Виды размерных цепей Линейная размерная цепь — размерная цепь, звеньями которой являются линейные размеры. Угловая размерная цепь — размерная цепь, звеньями которой являются угловые размеры. Размерная цепь с параллельными звеньями — размерная цепь, все звенья которой параллельны (см. задания 7.1 и 7.2). Плоская размерная цепь — размерная цепь, звенья которой расположены в одной или нескольких параллельных плоскостях. Пространственная размерная цепь — размерная цепь, звенья которой расположены в пространстве под различными углами. Размерная цепь любого вида может быть преобразована к размерной цепи с параллельными звеньями, т.е. методика решения этого вида цепи универсальна. Составляющие, замыкающие и исходные звенья характеризуются: · действительным, предельным (наибольшим A 0 max, Аk mах и наименьшим A 0 min, Аk min) и номинальным (A 0, Аk) размерами; · верхним Es(A 0), ES (Аk) и нижним EI(A 0), EI (Аk) отклонениями; · допусками (ТА0, TAk) и их полями допусков. Схема размерной цепи представляет собой графическое изображение размерной цепи (см. задания 7.1 и 7.2).
Методы расчета размерных цепей Размерные цепи рассчитывают на полную взаимозаменяемость методом максимума-минимума и на неполную взаимозаменяемость вероятностным методом. При расчете размерных цепей встречаются две основных задачи: 1) по установленным размерам, отклонениям и допуску исходного размера определяют предельные размеры, отклонения и допуски составляющих размеров (прямая задача). 2) по установленным размерам и допускам составляющих звеньев определяют номинальный и предельные размеры замыкающего звена, его допуск и предельные отклонения (обратная задача). Расчет на максимум-минимум. Данный метод расчета основан на предположении, что при сборке механизма возможно сочетание увеличивающих звеньев, изготовленных по наибольшим предельным размерам с уменьшающими звеньями, изготовленными но наименьшим предельным размерам или наоборот. Этот метод расчета обеспечивает полную взаимозаменяемость в процессе сборки и эксплуатации изделий. Однако допуски составляющих размеров, вычисленные по этому методу, особенно для размерных цепей, содержащих много звеньев, могут получиться в техническом и экономическом отношениях неоправдано малыми. Поэтому данный метод применяют для проектирования размерных цепей, имеющих малое число составляющих звеньев невысокой точности.
Основные уравнения размерной цепи Номинальный размер замыкающего звена размерной цепи
где n и р — число соответственно увеличивающих и уменьшающих звеньев. Наибольший предельный размер замыкающего звена
Наименьший предельный размер замыкающего звена
Верхнее предельное отклонение замыкающего (исходного) размера
Нижнее предельное отклонение замыкающего (исходного) размера
Допуск замыкающего (исходного) звена
В соответствии с ЕСКД значение допуска любого размера ТАk = аk×ik, где аk – количество стандартизованных единиц допуска, установленных для квалитетов:
ik – единицы допуска, установленные для интервалов номинальных размеров:
В общем случае для разных звеньев размерной цепи могут быть приняты любые значения аk, что означает различный уровень относительной точности. В частности, в соответствии со способом равных допусков принимают ТАk одинаковыми для всех звеньев цепи. Тогда, очевидно, для соблюдения правил ЕСКД аk придется подбирать различным по величине и нестандартным. Однако это не оптимально с экономической точки зрения, т.к. обычно для более мелких по размеру поверхностей достичь общего уровня абсолютной точности будет легче, чем для более крупных. Более целесообразным считается способ равноточных допусков, при котором все составляющие звенья размерной цепи имеют равную относительную точность, т.е. должны выполняться по одному квалитету, и иметь одинаковое значение аk – среднее количество единиц допуска аkср для каждого составляющего размера:
Это значение далее округляют до ближайшего стандартного, соответствующего одному из квалитетов (см. таблицу выше). После этого по справочным таблицам полей допусков ЕСДП, например [1], определяют в соответствии с выбранным квалитетом отклонения на составляющие звенья размерной цепи. При этом возможны ряд вариантов выбора конкретного поля допуска при одном и том же квалитете. Обычно доопределяют эту неопределенность выбором какой-либо стратегии или по конструктивно-технологическим критериям исходя из назначения поверхностей, размеры которых входят в состав цепи. В данной контрольной работе рекомендуется использовать следующую, часто применяемую стратегию: на увеличивающие звенья размерной цепи отклонения назначаются как для основных отверстий, т.е. по полю допуска Н, а на меньшающие звенья размерной цепи – как для основных валов, т.е. по полю допуска h. При округлении количества единиц допуска аkср до ближайшего стандартного значения рассмотренный выше баланс допусков и отклонений не соблюдается:
Для выполнения баланса требуется осуществить коррекцию отклонений составляющих звеньев размерной цепи на основании расчета. В общем случае для этого допуск и отклонения одного или нескольких звеньев принимают нестандартными, не соответствующими стандартизованным полям допусков. Такие звенья размернойцепи называют компенсирующими. Понятно, что такое решение обычно снижает уровень стандартизации размеров, осложняет и удорожает изготовление изделия. Чтобы снизить негативный эффект от этого шага, стараются в качестве компенсирующего звена выбирать только одно из составляющих звеньев. Выбор компенсирующего звена – задача нетривиальная, часто решается на основе опыта конструктора-технолога, исходя из назначения поверхностей, размеры которых входят в состав цепи, или на основании какой-либо стратегии. В данной контрольной работе рекомендуется в качестве компенсирующего звена выбирать составляющее звено с наибольшим значением номинального размера. В этом случае величина абсолютной компенсации наименьшая, а, значит, и минимален риск невозможности решения задачи или чрезмерного ужесточения допуска на компенсирующее звено. Примеры: 1. Найти номинальный размер и отклонения замыкающего звена Х методом полной взаимозаменяемости (обратная задача) для размерной цепи:
Решение: Определяем, что размер Номинальный размер замыкающего звена размерной цепи
По таблицам полей допусков [1] находим предельные отклонения, допуски и предельные размеры составляющих звеньев: ES ( EI ( T (
ES ( EI ( T (
Наибольший предельный размер замыкающего звена
Наименьший предельный размер замыкающего звена
Верхнее предельное отклонение замыкающего размера
Нижнее предельное отклонение замыкающего размера
Допуск замыкающего звена
2. Найти номинальный размер замыкающего звена Х+0,400 и отклонения составляющих звеньев методом полной взаимозаменяемости (прямая задача) для размерной цепи:
Решение: Определяем, что размер Предельные отклонения и допуск исходного звена Х:
Находим среднее количество единиц допуска для каждого составляющего размера, полагая, что все составляющие размеры размерной цепи имеют равную относительную точность (способ равноточных допусков), т.е. должны выполняться по одному квалитету:
что соответствует 11 квалитету. Значит, назначаем допуски на составляющие размеры по этому квалитету. Определяем значения отклонений и допуск звена ES ( EI ( T ( Принимаем в качестве компенсирующего звена
следовательно
следовательно
T ( Производим окончательную проверку: Т (А 0) = Проверка показывает, что расчет произведен верно. Окончательно полученные размеры составляющих звеньев размерной цепи:
|

 .
. .
. .
. .
. .
. .
. .
. .
. ,
, ;
; .
. .
.
 = 85 n 9 является увеличивающим, а размер
= 85 n 9 является увеличивающим, а размер  = 60 е 10 – уменьшающим.
= 60 е 10 – уменьшающим. = 85 – 60 = 25 мм.
= 85 – 60 = 25 мм. = 85 + 0,110 = 85,110 мм,
= 85 + 0,110 = 85,110 мм, = 85 + 0,023 = 85,023 мм,
= 85 + 0,023 = 85,023 мм, = 60 + (–0,060) = 59,940 мм,
= 60 + (–0,060) = 59,940 мм,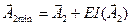 = 60 + (–0,180) = 59,820 мм,
= 60 + (–0,180) = 59,820 мм, =
=  –
–  = 85,110 – 59,820 = 25,290 мм.
= 85,110 – 59,820 = 25,290 мм.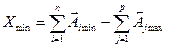 =
=  –
–  = 85,023 – 59,940 = 25,083 мм.
= 85,023 – 59,940 = 25,083 мм. =
=  –
–  = 0,110 – (–0,180) = 0,290 мм,
= 0,110 – (–0,180) = 0,290 мм, =
=  –
–  = 0,023 – (–0,060) = 0,083 мм.
= 0,023 – (–0,060) = 0,083 мм. = T (
= T (
 = 85 – увеличивающий, а
= 85 – увеличивающий, а  = 40 – уменьшающий.
= 40 – уменьшающий. = +0,400 мм,
= +0,400 мм, = 0,000 мм,
= 0,000 мм, = 0,400 – 0,000 = 0,400 мм = 400 мкм.
= 0,400 – 0,000 = 0,400 мм = 400 мкм. +
+  = T (
= T (


