КАЛИНИНГРАДСКИЙ ИНСТИТУТ ЭКОНОМИКИ ФИЛИАЛ САНКТ-ПЕТЕРБУРГСКОЙ АКАДЕМИИ УПРАВЛЕНИЯ И ЭКОНОМИКИ
. Построим на плоскости 4 точки и обозначим их
Рис. 22. Изоморфный орграф G = (X, U). Так как Теперь запишем матрицу инцидентности С для орграфа G. Построенный орграф G = (X, U) имеет 4 вершины и 12 дуг, т.е. Х={ U= Матрица инцидентности орграфа G будет иметь 4 строки и 12 столбцов
Петле соответствует нулевой столбец. Матрица инцидентности только указывает на наличие петель в орграфе, но не указывает, каким вершинам эти петли инцидентны.
3. Задана симметрическая матрица А неотрицательных целых чисел.
1. Нарисовать на плоскости граф 2. Нарисовать на плоскости орграф А=
Решение1. Напомним, что матрицей смежности графа
Построим граф Поскольку данная матрица является симметрической матрицей четвертого порядка с неотрицательными элементами, то ей соответствует неориентированный граф с четырьмя вершинами. Расположив вершины А=
Рис. 3 Граф G=(X,U) Теперь найдем матрицу инцидентности графа G =(X,U). Напомним определение матрицы инцидентности графа G=(X,U) с множеством вершин
2. Заданная матрица А имеет 4 строки и 4 столбца, следовательно орграф имеет 4 вершины. Обозначим их соответственно
На плоскости строим 4 точки. Обозначим их через
Рис. 4. Изоморфный орграф G=(X,U). Так как Теперь запишем матрицу инцидентности С для орграфа G. Построим орграф G=(X,U) имеет 4 вершины и 17 дуг, т.е.
Матрица инцидентности орграфа G будет иметь 4 строки и 17 столбцов
4. Заданная формула Решение. Как известно, все формулы логики высказываний можно записать при помощи пропозициональных связок:
Используя равенства (1) – (3) и основные законы 21 – 30. Задана симметрическая матрица A неотрицательных целых чисел. 1. Нарисовать на плоскости граф G=(X,U) (единственный с точностью до изоморфизма), имеющий заданную матрицу А своей матрицей смежности. Найти матрицу инцидентности графа G. 2. Нарисовать на плоскости орграф G=(X,U) (единственный с точностью до изоморфизма)? Имеющий заданную матрицу А своей матрицей смежности. Найти матриц инцидентности Орграфа G. 21.
23.
25.
27.
29.
КАЛИНИНГРАДСКИЙ ИНСТИТУТ ЭКОНОМИКИ ФИЛИАЛ САНКТ-ПЕТЕРБУРГСКОЙ АКАДЕМИИ УПРАВЛЕНИЯ И ЭКОНОМИКИ
|

 ,
,  ,
,  ,
,  .
.
 , то при вершине
, то при вершине  нет петель,
нет петель,  , значит из вершины
, значит из вершины  . Рассуждая таким же образом, построим геометрический орграф, изоморфный орграфу G = (X, U), для которого матрица В является матрицей смежности (рис. 22).
. Рассуждая таким же образом, построим геометрический орграф, изоморфный орграфу G = (X, U), для которого матрица В является матрицей смежности (рис. 22). .
.
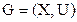 (единственный с точностью до изоморфа), имеющий заданную матрицу А своей матрицей смежности. Найти матрицу инцидентности
(единственный с точностью до изоморфа), имеющий заданную матрицу А своей матрицей смежности. Найти матрицу инцидентности  графа G.
графа G.
 орграфа G.
орграфа G.
 называется матрица
называется матрица  размера
размера  , в которой элемент
, в которой элемент  равен числу ребер в G, соединяющих
равен числу ребер в G, соединяющих 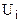 с
с  . Матрица смежности графа G является симметрической, то есть
. Матрица смежности графа G является симметрической, то есть на плоскости произвольным образом (рис. 3), соединяем их с учетом кратности ребер.
на плоскости произвольным образом (рис. 3), соединяем их с учетом кратности ребер.


 и множеством ребер
и множеством ребер  Так называется матрица
Так называется матрица  размера
размера  , у которой
, у которой

 а матрицу представим в виде
а матрицу представим в виде



 то при вершине
то при вершине  имеется петля;
имеется петля;  значит, из вершины
значит, из вершины  выходят две стрелки к вершине
выходят две стрелки к вершине  и т.д. (рис.4).
и т.д. (рис.4).


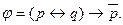 От формулы
От формулы  перейти к эквивалентной ей формуле
перейти к эквивалентной ей формуле  так, чтобы формула
так, чтобы формула  » и «
» и « ». Исходя из истинностных таблиц, доказать, что формулы
». Исходя из истинностных таблиц, доказать, что формулы  т.е. пропозициональные связки
т.е. пропозициональные связки  могут быть определены в терминах связок
могут быть определены в терминах связок  Можно доказать, что
Можно доказать, что (1)
(1) (2)
(2) (3)
(3)

 22.
22. 

 24.
24. 

 26.
26. 
 28.
28. 
 30.
30. 



