Примеры решения задач. Пример 1. Материальная точка массой 1,0 г совершает гармонические колебания
Пример 1. Материальная точка массой 1,0 г совершает гармонические колебания. Наибольшее отклонение точки от положения равновесия равно 10 см, наибольшая скорость равна 20 см/с. Найти циклическую частоту колебаний и максимальные значения ускорения точки и ее кинетической и потенциальной энергии, а также полную механическую энергию этой точки.
Дано: m=1,0 г =10-3 кг; А =10 см = 10-1 м; Найти: Решение. Используя уравнение гармонических колебаний
найдем скорость материальной точки как первую производную от смещения х по времени t:
Максимальное значение скорости
Так как, по определению, максимальное смещение
Ускорение колеблющейся материальной точки найдем как первую производную от скорости υ по времени t:
Максимальное значение ускорения
Как указывалось ранее в разделе Основные теоретические сведения, кинетическая энергия колеблющейся материальной точки определяется по формуле:
а ее потенциальная Еп и полная механическая энергия Е соответственно по формулам:
и
Поэтому, учитывая, что максимальное значение функций
Произведем расчет искомых величин, используя условия задачи:
Проверим размерность:
В дальнейшем проверка размерности производиться не будет, так как она осуществляется аналогичным образом. Ответ:
Пример 2. Тонкий однородный обруч радиусом 50 смподвешен на вбитый в стену гвоздь и совершает колебания в плоскости, параллельной стене. Определить период таких колебаний.

Как известно, период малых колебаний физического маятника определяется по формуле:
Момент инерции такого маятника находится по теореме Штейнера:
где Поэтому
Следовательно,
Произведем расчет искомой величины:
Ответ: T =2,0 с.
Пример 3. Найти уравнение колебания, получающегося в результате сложения двух гармонических колебаний одного направления с одинаковыми периодами колебаний, равными 1,5с, и имеющими одинаковые амплитуды, равные 2,0 см. Начальная фаза первого колебания равна
Дано: Т1=Т2= 1,5 с; Найти: Решение. По условию задачи складываются колебания одинакового направления и одинаковой частоты (периоды колебаний являются одинаковыми), поэтому уравнение результирующего колебания должно иметь вид:
При этом амплитуда результирующего колебания:
а циклическая частота:
где период результирующего колебания: Т0=Т1=Т2. Тангенс начальной фазы:
а начальная фаза:
Произведем расчет искомых величин, используя условия задачи:
Поэтому искомое уравнение:
Ответ:
Пример 4. Материальная точка участвует одновременно в двух гармонических колебаниях одинаковой частоты, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями Дано: А, В, ω0; Найти: Решение. Используя известные из тригонометрии формулы приведения, можно записать:
Поэтому
Аналогично
Возведем два последних уравнения в квадрат:
и сложим затем почленно их левые и правые части с учетом основного тригонометрического тождества:
Следовательно,
Ответ: Пример 5. Материальная точка совершает затухающие колебания, логарифмический декремент затухания которых равен 3,00∙10-3. Определить число полных колебаний, которые должна совершить точка, чтобы амплитуда колебаний уменьшилась в два раза.
Дано: Найти: N. Решение. Как известно, амплитуда затухающих колебаний
Поэтому
Так как логарифмический декремент затухания
то коэффициент затухания
Следовательно, подставляя формулу (2) в уравнение (1), получим:
Поэтому
Откуда
Целая часть отношения Поэтому
Произведем расчет искомой величины:
Ответ: N= 231.
Пример 6. Материальная точка массой 2,0 г при совершении в некоторой среде затухающих колебаний колеблется с циклической частотой 100 с-1. При совершении вынужденных колебаний в этой среде материальная точка при резонансе колеблется с циклической частотой 99 с-1 под действием периодически изменяющейся силы, амплитудное значение которой равно 20 мН. Определить резонансную амплитуду колебаний этой точки. Дано: m =2,0 г =2,0∙10-3 кг; ω=100 с-1, ωр=99 с-1, Найти: Ар. Решение. Как известно,
а циклическая частота затухающих колебаний
то, следовательно,
Учитывая, что
получим, возведя формулы (2) и (4) квадрат:
Поэтому
Отсюда
Так как
то подставляя формулы (7) и (8) в формулу (3), получим:
Произведем расчет искомой величины:
Ответ: Ар= 0,35 см.
Пример 7. Плоская волна распространяется в однородной упругой среде с фазовой скоростью 10 м/с. Максимальные значения скорости и ускорения материальных точек среды, в которой распространяется волна, составляют соответственно 2,00·10-2 м/с и 1,26 м/c2.Определить длину этой волны.
Дано: υ=10 м/с; Найти: λ. Решение. Уравнение плоской волны, распространяющейся в положительном направлении оси х, имеет вид:
Поэтому
Так как максимальные значения
и
то
Следовательно,
Длина волны
Подставляя формулу (5) в выражение (6), получим:
Произведем расчет искомой величины:
Ответ:λ=1 м.
Пример 8. На плоскую поверхность однородного прозрачного тела с показателем преломления 1,50 нанесена тонкая однородная прозрачная пленка с показателем преломления 1,60. На пленку под углом падения 60° падает монохроматический свет с длиной волны 700 нанометров. При какой минимальной толщине пленки отраженные лучи будут максимально усилены, если тело находится в воздухе.
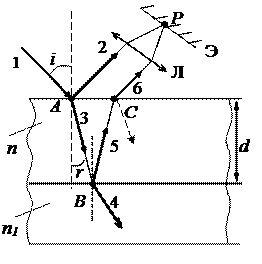
При падении луча 3 на нижнюю границу пленки (точку В, рисунок 20) часть света снова преломится (луч 4), уйдет в прозрачную среду с показателем преломления n1 и не будет участвовать в интерференции, а часть- отразится от нижней границы пленки в точке В (луч 5). На верхней границе пленки, в точке С, часть света снова отразится (этот луч на рисунке 20 показан пунктиром), а часть преломится (луч 6). Лучи 2 и 6, пройдя собирающую линзу Л будут интерферировать, например, в точке Р на экране э, установленном в фокальной плоскости этой линзы. Так как показатель преломления воздуха меньше, чем пленки, а показатель преломления пленки больше, чем показатель преломления тела, на которое нанесена эта пленка, то фаза колебаний будет меняться наπ только при отражении света в точке А. Поэтому оптическая разность хода лучей 2 и 6 определится по формуле:
Так как по условию задачи эти лучи при интерференции должны максимально усиливать друг друга, следовательно, Δ L= 2 m( λ / 2 ) (2) Приравняв правые части формул (1) и (2), найдем толщину пленки d:
Минимальная толщина пленки будет наблюдаться при m, равном 0. Следовательно,
Произведем расчет искомой величины:
Ответ: d min=520 нм. Пример 9. С помощью дифракционной решетки с периодом d, равным 20·10-6м, требуется разрешить дублет натрия (λ1 равна 589,0 ·10-9м и λ2 равна 589,6·10-9м) в спектре второго порядка. При какой наименьшей длине
Дано: λ1 =589,0 · 10-9м; λ2 = 589,6 · 10-9м; m =2; d = 20·10-6м. Найти: Решение. Длины волн дублета натрия λ1 и λ2 очень близки друг другу. Поэтому разрешающая способность решетки:
где
а N - минимально необходимое число щелей такой решетки, которое должно укладываться на ее длине. Следовательно,
Отсюда
Поэтому, используя формулы (1), (2), (4), можно получить:
Произведем расчет искомой величины:
Ответ:
Пример 10. Определить показатель преломления стекла, если при отражении от него света отраженный луч полностью поляризован при угле преломления 35°. Стекло находится в воздухе.
Дано: r = 35°. Найти: n. Решение. Так как отраженный луч полностью поляризован (рисунок 21), то свет падает на границу раздела стекло- воздух под углом Брюстера, а угол между отраженным и преломленным лучами равен 90°. По первому закону геометрической оптики угол отражения равен углу падения. Поэтому, как следует из рисунка 21,
Ответ:
|

 м/c.
м/c. .
. ,
, .
. будет определяться максимальным значением функции
будет определяться максимальным значением функции 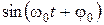 , которое, как известно, равно единице. Поэтому
, которое, как известно, равно единице. Поэтому .
. равняется амплитуде, то
равняется амплитуде, то .
. .
. будет определяться максимальным значением функции
будет определяться максимальным значением функции  , которое, как известно, равно единице. Поэтому
, которое, как известно, равно единице. Поэтому .
. ,
,
 .
.
 c-1.
c-1. м/с2.
м/с2. .
. ;
;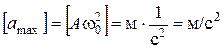 ;
; .
. ;
;  ;
; .
. .
. ,
, - момент инерции маятника (обруча массой m в нашем случае) относительно оси вращения, проходящей через его центр масс (точку С на рисунке 19);
- момент инерции маятника (обруча массой m в нашем случае) относительно оси вращения, проходящей через его центр масс (точку С на рисунке 19);  - расстояние между осями, проходящими через точки О и С, которое, как следует из рисунка 22, практически равно радиусу обруча R.
- расстояние между осями, проходящими через точки О и С, которое, как следует из рисунка 22, практически равно радиусу обруча R. .
.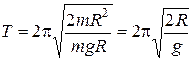 .
. с
с , а начальная фаза второго колебания равна
, а начальная фаза второго колебания равна  .
. ;
;  ;
;  .
. .
. .
. ,
, ,
, ,
, .
.
 с-1;
с-1;
 .
. и
и  . Определить уравнение траектории точки.
. Определить уравнение траектории точки. .
. .
.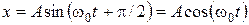 .
. .
. .
. ;
;
 .
.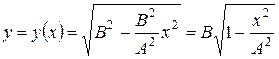 .
. .
. ;
;  .
. .
. (1)
(1) ,
, . (2)
. (2) .
.
 .
.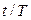 определяет искомое число колебаний N.
определяет искомое число колебаний N. .
. .
. .
. , (1)
, (1) , (2)
, (2) . (3)
. (3) , (4)
, (4)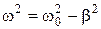 (5)
(5) (6)
(6)
 (7)
(7) , (8)
, (8) . (9)
. (9)
 ;
; 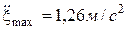 .
.
 , (1)
, (1) . (2)
. (2)
 ,
, (3)
(3)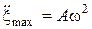 (4)
(4) (5)
(5) (6)
(6)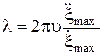 . (7)
. (7) .
.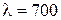 нм
нм  ; i =60°; n =1,60; n1 =1,50.
Найти: d min.
Решение. При отражении от границ тонкой пленки максимальное усиление света будет достигаться тогда, когда на оптической разности хода интерферирующих лучей будет укладываться четное число длин полуволн. Пусть, например, один из лучей (луч 1, рисунок 20) светового потока падает на пленку в точку А, где часть света отразится (луч 2), а часть преломится (луч 3).
; i =60°; n =1,60; n1 =1,50.
Найти: d min.
Решение. При отражении от границ тонкой пленки максимальное усиление света будет достигаться тогда, когда на оптической разности хода интерферирующих лучей будет укладываться четное число длин полуволн. Пусть, например, один из лучей (луч 1, рисунок 20) светового потока падает на пленку в точку А, где часть света отразится (луч 2), а часть преломится (луч 3).
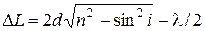 , (1)
, (1)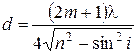 .
. .
. .
. решетки это возможно?
решетки это возможно? .
. , (1)
, (1) , (2)
, (2) (3)
(3) (4)
(4) .
.
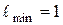 см.
см. .
Следовательно, по закону Брюстера
.
Следовательно, по закону Брюстера
 ,
где показатель преломления воздуха n0 примерно равен1.
Поэтому
,
где показатель преломления воздуха n0 примерно равен1.
Поэтому
 ,
то есть
,
то есть
 .
.

 .
.


