Затухающие механические колебания
Свободные колебания, амплитуда которых уменьшается с течением времени вследствие потерь энергии в окружающую среду, называются затухающими. Уравнение затухающих механических колебаний имеет следующий вид:
где х - смещение, А0 - начальная амплитуда в момент времени, равный нулю; β - коэффициент затухания, который определяется коэффициентом сопротивления r и массой m колеблющейся материальной точки:
ω- частота затухающих колебаний:
где t - время; Период затухающих колебаний
Как следует из уравнения затухающих колебаний и рисунка 9, амплитуда А затухающих колебаний (пунктирная линия на рисунке 9) экспоненциально уменьшается с течением времени:
Время τ, в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации. Учитывая, что амплитуда затухающих колебаний спустя время, равное времени релаксации
Получим, исходя из определения времени релаксации, что
Поэтому время релаксации
Следовательно, время релаксации обратно пропорционально коэффициенту затухания β. Величина, равная натуральному логарифму отношения значений амплитуд, соответствующих моментам, отличающимся по времени на период, называется логарифмическим декрементом затухания:
То есть
Следовательно, логарифмический декремент затухания возрастает при увеличении коэффициента затухания β и периода Т колебаний.
|

 ,
,
 ;
; ,
, - начальная фаза колебаний.
- начальная фаза колебаний. .
.

 ,
,
 .
.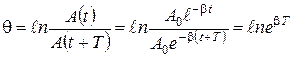 .
. .
.


