Сложение гармонических колебаний. одинакового направления и одинаковой частоты
одинакового направления и одинаковой частоты
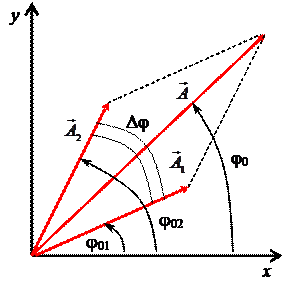
При сложении гармонических колебаний одинакового направления и одинаковой частоты обычно используется метод векторных диаграмм.
Модуль такого вектора равен амплитуде соответствующего колебания, а его проекция на выбранное направление, например, на ось х (рисунок 7), будет совершать гармонические колебания:
где φ – угол между вектором Обозначив проекцию Ах через х, получим уравнение гармонических колебаний:
При сложении двух гармонических колебаний одинакового направления и одинаковой циклической частоты, происходящих, например, вдоль оси х, первое из которых описывается уравнением:
а второе - уравнением
где х1, х2 - смещения; А1, А2 - амплитуды;
|
(рисунок 7), вращающийся относительно своего начала с угловой скоростью, равной циклической частоте ω0 этого колебания.
,
.
,
,
, 
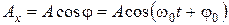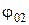- начальные фазы соответствующих колебаний; t - время, результирующее колебание будет происходить также вдоль оси х с той же циклической частотой ω0 в соответствии с уравнением
,
.
