Контрольное задание №3 по разделу
«Теория вероятностей и математическая статистика» Вариант 2 1. Известны вероятности несовместных событий а) в)
2. Внутрь квадрата наудачу брошена точка. Найти вероятность того, что точка окажется внутри окружности, которая вписана в квадрат.
3. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5?
4. В теннисном турнире участвуют 10 спортсменов. Сколькими способами теннисисты могут завоевать золото, серебро и бронзу?
5. Сколько отрезков соединяют каждую вершину выпуклого семиугольника с остальными вершинами?
6. В урне находятся 49 шариков, из которых 17 белых. Потеряли 2 не белых шарика. Найти вероятность того, что выбранный наугад шарик будет не белым.
7. Среди 6 приборов имеется два неисправных. Приборы проверяются по очереди до выявления первого неисправного. Найти вероятность того, что эксперимент закончится на третьем приборе. 8. В урне 2 белых и 2 черных шара. Извлекают по очереди два шара, причем после первого извлечения шар возвращается в урну. Найти вероятность того, что оба шара белые. 9. Бросают игральную кость до появления на грани кубика 3 очков. Найти вероятность того, что эксперимент закончится на третьем броске. 10. Событие 11. Имеется пять винтовок, три из которых снабжены оптическим прицелом. Вероятность попадания в цель при выстреле из винтовки с оптическим прицелом, равна 0,95, для винтовки без оптического прицела – 0,7. Найти вероятность того, что цель поражена из винтовки без оптического прицела. 12. Дан графический закон распределения дискретной случайной величины (многоугольник распределения). Записать ряд распределения случайной величины
13. Дискретная случайная величина принимает значения 2, 5, 10 с соответствующими вероятностями 0,3, 14. Дан ряд распределения случайной величины:
Найти моду случайной величины 15. Дан график функции распределения
16. Дан ряд распределения случайной величины
17. В урне 2 белых и 2 черных шара. Шары извлекаются из урны без возвращения до появления черного шара. Случайная величина 18. Игральную кость бросают 45 раз. Случайная величина 19. Дана функция плотности распределения вероятностей случайной величины 20. Случайная величина 21. Случайная величина
22. Случайная величина 23. Случайная величина 24. Закон распределения случайной величины
25. Функция плотности распределения вероятностей случайной величины
|

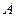 ,
, 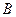 ,
, 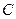 . Указать вероятности событий, которые образуют полную группу
. Указать вероятности событий, которые образуют полную группу ,
,  ,
,  б)
б) 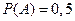 ,
, 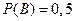 ,
,  ,
, 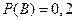 ,
, 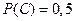 г)
г) 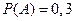 ,
,  и
и 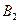 , образующих полную группу событий. Известны вероятность
, образующих полную группу событий. Известны вероятность  и условные вероятности
и условные вероятности  ,
,  . Найти вероятность события
. Найти вероятность события 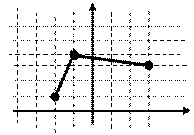
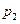 , 0,6. Найти математическое ожидание случайной величины.
, 0,6. Найти математическое ожидание случайной величины.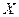

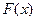 случайной величины
случайной величины  со значениями
со значениями 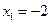 и
и  . Найти вероятность значения
. Найти вероятность значения 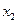
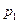
 . Математическое ожидание
. Математическое ожидание 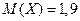 , дисперсия
, дисперсия 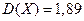 . З Найти значение случайной величины
. З Найти значение случайной величины 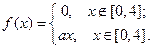 Найти значение параметра
Найти значение параметра 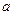
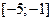 . Найти дисперсию случайной величины.
. Найти дисперсию случайной величины.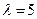 . Записать функцию распределения вероятностей случайной величины.
. Записать функцию распределения вероятностей случайной величины.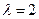 . Найти среднее квадратичное отклонение случайной величины.
. Найти среднее квадратичное отклонение случайной величины.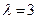 . Найти вероятность попадания случайной величины в интервал
. Найти вероятность попадания случайной величины в интервал 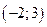 .
. . Найти математическое ожидание случайной величины.
. Найти математическое ожидание случайной величины. . Записать уравнение оси симметрии кривой Гаусса.
. Записать уравнение оси симметрии кривой Гаусса.


