Механические колебания и волны
• Уравнение гармонических колебаний
где А – амплитуда колебаний, • Циклическая частота
• Скорость точки, совершающей гармонические колебания
• Ускорение точки, совершающей гармонические колебания
• При сложении колебаний одного направления и одинаковой частоты - результирующая амплитуда колебаний находится по формуле:
- начальная фаза результирующего колебания
• Дифференциальное уравнение колебаний материальной точки
• Период колебаний пружинного маятника
где m- масса груза, k –коэффициент упругости пружины
• Период колебаний математического маятника
где g – ускорение свободного падения,
• Период колебаний физического маятника
где L – приведённая длина физического маятника, J- момент инерции,
• Полная энергия гармонических колебаний
• Уравнение затухающих колебаний
где • Частота затухающих колебаний
где • Логарифмический декремент затухания
• Резонансная частота колебаний
|
,
-циклическая частота, t- время, 
-начальная фаза колебаний,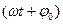 
- фаза колебаний;
, 
- период колебаний;
) 
;
;
;
;
,
- длина нити маятника;
,
;
,
- зависимость амплитуды колебаний от времени t; А0 – начальная амплитуда; е – основание натурального логарифма; 
- коэффициент затухания; r – коэффициент сопротивления;
,
- частота свободных колебаний
;
