КОНТРОЛЬНАЯ РАБОТА №3
ЗАДАЧА 1. Материальная точка массой 20 г совершает гармонические колебания с периодом 9 с. Начальная фаза колебаний 100. Через какое время от начала движения смещение точки достигнет половины амплитуды? Найти амплитуду, максимальные скорость и ускорение точки, если её полная энергия равна 10-2Дж.
m =2·10-2кг Уравнение гармонического колебания точки Т =9 с
х= 0,5 А Е = 10-2Дж Искомое время ______________ Амплитуду колебаний определяем из выражения для t, А, Vmax, энергии amax-? Зная амплитуду, можно определить максимальную скорость и ускорение точки, которые вычисляются по формулам
Проверка размерности:
Вычисления:
Ответ:
ЗАДАЧА 2. Напряжение на обкладках конденсатора в колебательном контуре изменяется по закону 10 мкФ. Найти индуктивность контура и закон изменения силы тока в нем.
С = 10-5 Ф контуре изменяется по гармоническому закону ______________ L-?, I=I(t)
Индуктивность Заряд на обкладках конденсатора вычисляется по формуле
По определению сила тока – производная заряда по времени
Вычисления:
Ответ:
ЗАДАЧА 3. Колеблющиеся точки, находящиеся на одном луче, удалены от источника колебаний на 8м и 11м и колеблются с разностью фаз 3π/4. Период колебания источника 10-2с. Чему равна длина волны и скорость распространения колебаний в данной среде? Составить уравнение волны для первой и второй точек, считая амплитуды колебаний точек равными 0,25 м.
Δφ = 3π/4 Разность фаз двух колебаний двух точек в волне Т = 10-2с определяется по формуле А1= А2 =0,25 м ______________ λ -? V -? y1= у (t) y2= у (t) Проверка размерности:
Вычисления:
Уравнения
Ответ:
ЗАДАЧА 4. Какую наименьшую толщину должна иметь мыльная пленка, чтобы отраженные лучи имели красную окраску (
λкрас=0,63·10-6м Условие максимума освещенности при интерференции
n = 1,33 λ – длина волны. ______________ При интерференции на тонкой пленке толщиной d, dmin-? обладающей показателем преломления n, в отраженном свете разность хода лучей определяется по формуле
Минимальная толщина пленки будет при к = 1. Тогда
Вычисления:
Ответ:
ЗАДАЧА 5. Постоянная дифракционной решетки 2,5 мкм. Определить наибольший порядок спектра, общее число главных максимумов в дифракционной картине и угол дифракции в спектре 2-го порядка при нормальном падении монохроматического света с длиной волны 0,62 мкм.
d = 2,5·10-6м Условия максимума освещенности при дифракции на k =2 решетке λ= 6,2·10-7м Угол φ может принимать максимальное значение 900, т.е. ______________ kmax-? N -? φ2 -? Общее число максимумов Угол дифракции φ2 определяется по формуле
Вычисления:
Ответ:
ЗАДАЧА 6. Интенсивность естественного света, прошедшего через призму Николя, уменьшилась в 2,3 раза. Во сколько раз она уменьшится, если за первой призмой поставить вторую такую жепризму, так, чтобы угол между их главными плоскостями был равен 600?
Дано Решение
______________ необыкновенный, поэтому каждый из лучей обладает энергией I0/2. Обыкновенный отражается и
выходит из призмы уменьшая свою интенсивность на После прохождения второго поляризатора (анализатора) интенсивность света уменьшается как за счет отражения и поглощения света, так и из-за несовпадения плоскостей поляризации двух поляризаторов. В соответствии с законом Малюса с учетом потерь интенсивность света на выходе из анализатора равна Находим во сколько раз уменьшается интенсивность света
Выражаем из (1)
Подставляем (3) в (2)
Вычисления:
Ответ:
ЗАДАЧА 7. Во сколько раз увеличится мощность излучения черного тела, если максимум энергии излучения сместится с красной границы видимого спектра к его фиолетовой границе (λкрас= 0,76 мкм, λфиол= 0,38 мкм).
λкрас= 0,76 ·10-6м Максимальная длина волны, приходящаяся на максимум λфиол= 0,38·10-6м энергии излучения черного тела, согласно закону ______________ смещения Вина Nфиол/Nкрас при которой максимум энергии излучения приходится на красную и фиолетовую границы спектра Ткрас= b/ λкрас; Тфиол= b/ λфиол. Мощность излучения вычисляется по формуле N = R·S. По закону Стефана – Больцмана R = σТ4. Для температуры Ткрас и Тфиол
Откуда Вычисления:
Ответ:
ЗАДАЧА 8. Фотон с длиной волны
Дано: Решение
_________________
Искомое выражение
|

 Дано Решение
Дано Решение ,
,  (1))
(1))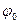 =100= π/18 Из уравнения (1) определяем время колебаний t
=100= π/18 Из уравнения (1) определяем время колебаний t откуда
откуда  ,
, .
.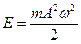
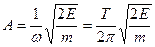 .
. и
и 
 ,
, 

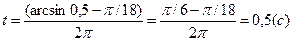 ,
, 
 (м/с),
(м/с),  (м/с2).
(м/с2). ,
,  ,
,  м/с,
м/с,  м/с2.
м/с2. (В). Емкость конденсатора
(В). Емкость конденсатора Дано Решение
Дано Решение , где
, где  - амплитудное значение напряжения.
- амплитудное значение напряжения. - циклическая частота. По условию
- циклическая частота. По условию . Отсюда
. Отсюда .
. ,
, .
. (Гн).
(Гн). (А)
(А) Гн,
Гн,  (А).
(А). Дано Решение
Дано Решение м Уравнение плоской волны
м Уравнение плоской волны м
м 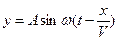
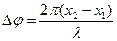 . Откуда длина волны
. Откуда длина волны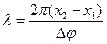 . Скорость распространения волны
. Скорость распространения волны . Циклическая частота
. Циклическая частота 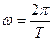
 ,
,  .
. ,
,  ,
,  с-1.
с-1.
 .
.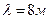 ,
,  ,
, 
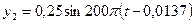 .
. )? Белый луч падает на пленку под углом 300(показатель преломления n = 1,33).
)? Белый луч падает на пленку под углом 300(показатель преломления n = 1,33). Дано Решение
Дано Решение
 , где Δ – разность хода, к – порядок максимума,
, где Δ – разность хода, к – порядок максимума,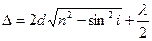 . Тогда условие максимума запишется
. Тогда условие максимума запишется , откуда
, откуда
 .
. (м).
(м). м.
м. Дано Решение
Дано Решение , где к = 0, 1, 2,….
, где к = 0, 1, 2,…. , тогда
, тогда  .
.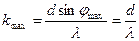 .
. .
. , откуда
, откуда  ,
, 
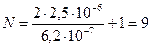 .
.  .
. 
 ,
,  ,
,  .
.

 Естественный свет, попадая в призму Николя
Естественный свет, попадая в призму Николя (поляризатор) раздваивается на луча – обыкновенный и
(поляризатор) раздваивается на луча – обыкновенный и поглощается зачерненной поверхностью, необыкновенный
поглощается зачерненной поверхностью, необыкновенный . На выходе из поляризатора интенсивность света
. На выходе из поляризатора интенсивность света  (1), где
(1), где 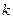 - коэффициент поглощения.
- коэффициент поглощения. .
. . (2)
. (2) (3)
(3) .
.
 .
. Дано Решение
Дано Решение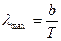 . Отсюда находит температуру,
. Отсюда находит температуру,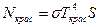 ,
, 
 .
. .
. .
. рассеялся на свободном электроне. Длина волны рассеянного фотона
рассеялся на свободном электроне. Длина волны рассеянного фотона  . Определить угол
. Определить угол  рассеяния.
рассеяния. Согласно эффекту Комптона
Согласно эффекту Комптона
 , где
, где  - комптоновская
- комптоновская длина волны. Если фотон рассеян на электроне, то
длина волны. Если фотон рассеян на электроне, то .
.

 ,
, .
.


