КОНТРОЛЬНАЯ РАБОТА № 4
ЗАДАЧА 1. В баллоне содержится азот массой
N2, He По закону Дальтона давление смеси газов равно сумме
Т = 300 К _____________ V -? Проверяем размерность: Вычисления: Ответ:
ЗАДАЧА 2. Определить коэффициент внутреннего трения для водорода, имеющего температуру 270С.
Н2 По определение коэффициент внутреннего трения
Т = 300 К арифметическая скорость молекул, <λ> - средняя d = 2,3·10-10м длина свободного пробега молекул. NA= 6,02·1023моль-1 Плотность ________________ η -? Плотность находим из уравнения Менделеева- Клапейрона Средняя арифметическая скорость По определению средняя длина свободного пробега
Давление и температура газа связаны соотношением R = 8,31 Дж/моль·К. Окончательно, выражение для коэффициента внутреннего трения имеет вид
Проверяем размерность: Вычисления:
Ответ:
ЗАДАЧА 3. Азот массой 2 кг охлаждают при постоянном давлении от 400 К до 300 К. Определить изменение внутренней энергии, внешнюю работу и количество выделенной теплоты.
N2 При изобарическом процессе изменение внутренней
Т1= 400 К Т2= 300 К i – число степеней свободы. Азот – двухатомный газ. Для m = 2 кг _____________ двухатомного газа i = 5. Тогда ΔU -? A-? Q -? Количество теплоты, выделяющееся при охлаждении газа при постоянном давлении теплоемкость при постоянном давлении. Для двухатомных молекул Количество теплоты Согласно первому началу термодинамики Вычисления:
Ответ:
ЗАДАЧА 4. Идеальный газ совершает цикл Карно. Температура нагревателя Т1= 500 К, холодильника Т2= 300 К. Работа изотермического расширения газа составляет 2 кДж. Определить: 1) термический КПД цикла; 2) количество теплоты, отданное газом при изотермическом сжатии холодильнику.
Дано Решение Т1= 500 К По определению КПД цикла Карно Т2= 300 К А12=2·103 Дж Откуда ______________ на совершение работы по расширению, т.е η -? Q2 -? Из уравнения (1) Проверяем размерность: Вычисления: Ответ:
ЗАДАЧА 5. В результате изотермического расширения объём 10 г кислорода увеличился в 3 раза. Определить изменение энтропии газа.
О2 Изменение энтропии системы определяется по формуле
m= 0,01 кг сообщенное телу; S1 и S2 – значение энтропии в Т - const начальном и конечном состоянии системы. V2 = 3V1 При изотермическом расширении все подводимое ______________ количество теплоты идет на работу по расширению ΔS -? газа Подставляя (2) в (1), получаем
Вычисления:
Ответ:
ЗАДАЧА 6. Определить наибольшую и наименьшую длины волн фотонов, излучаемых при переходе электронов в серии Пашена.
______________ электронов в атоме водорода можно с помощью формулы
В серии Пашена переход осуществляется на третью орбиту со всех вышележащих, т.е. m =3; n = 4,5,6,…,∞. Максимальное значение длины волны получаем при n = 4.
Ответ:
ЗАДАЧА 7. Определить период полураспада радиоактивного изотопа, если 5/8 начального количества ядер этого изотопа распалось за время 849с.
t = 849 c Закон радиоактивного распада
______________ T1/2 – период полураспада- время, за которое распадается T1/2-? половина исходного числа ядер. Из формулы (1) Проверяем размерность: Вычисление: Ответ: T1/2= 10 мин.
ЗАДАЧА 8. Ядро атома вора Дано Решение
mn= 1,008665 а.е.м. сохранения зарядового и массового чисел mLi= 7,016004 а.е.м. mHe= 4,002603 а.е.м. Изменение энергии при ядерной реакции в МэВ ΔЕ -? ΔЕ = Δmc2, массы. В атомных единицах массы (а.е.м.)
Вычисления: Поскольку масса исходных ядер больше массы получившихся, реакция сопровождается выделением энергии.
Ответ: ΔЕ = 2,17 МэВ.
ЗАДАЧА 9. Каков КПД атомной электростанции мощностью Р= 5·108Вт, если за 1 год было израсходовано m = 965 кг урана
Дано Решение Р= 5·108Вт Число атомов, содержащихся в массе m вещества t = 3,15·107c m = 956 кг Полная энергия, выделяющаяся при распаде N атомов ΔЕ = 3,2·10-11Дж урана μ = 235·10-3кг/моль Полная энергия, которую дает атомная электростанция _________________ η -? КПД – это отношение полезной энергии к полной энергии Проверяем размерность Вычисления: Ответ: η = 20%.
ЗАДАЧИ
|

 г и гелий массой
г и гелий массой  г. Давление смеси
г. Давление смеси 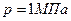 , температура Т = 300 К. Принимая данные газы за идеальные, определить объем сосуда.
, температура Т = 300 К. Принимая данные газы за идеальные, определить объем сосуда. Дано Решение
Дано Решение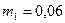 кг парциальных давлений газов, входящих в состав смеси.
кг парциальных давлений газов, входящих в состав смеси. кг
кг  . Каждый газ занимает весь объём.
. Каждый газ занимает весь объём. Согласно уравнению Менделеева -Клапейрона
Согласно уравнению Менделеева -Клапейрона
 ,
,  . Складывая левые и правые
. Складывая левые и правые части данных уравнений, получаем
части данных уравнений, получаем , откуда
, откуда 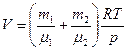
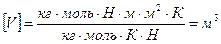


 Дано Решение
Дано Решение
 , где
, где  - плотность газа, <υ> -средняя
- плотность газа, <υ> -средняя , где V –объём.
, где V –объём. , откуда
, откуда  .
. .
. , где d – эффективный диаметр молекулы водорода, n0 – число молекул водорода в 1м3.
, где d – эффективный диаметр молекулы водорода, n0 – число молекул водорода в 1м3. , где
, где  ,
, .
. .
.
 .
. Дано Решение
Дано Решение энергии
энергии  .
. - молярная теплоемкость при постоянном объёме,
- молярная теплоемкость при постоянном объёме, .
.
 .
.  -молярная
-молярная .
. . Работу найдем исходя из первого начала термодинамики.
. Работу найдем исходя из первого начала термодинамики. , тогда
, тогда 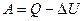
 (Дж),
(Дж), (Дж)
(Дж) (Дж)
(Дж) Дж,
Дж,  Дж,
Дж,  Дж.
Дж. или
или  .
.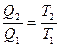 (1). Тепло, подводимое к системе идет
(1). Тепло, подводимое к системе идет .
. .
.
 ,
, 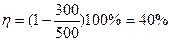 .
. ,
,  .
. Дано Решение
Дано Решение
 , (1) где
, (1) где  - количество теплоты,
- количество теплоты, . Давление выражаем из уравнения состояния
. Давление выражаем из уравнения состояния . Тогда
. Тогда  (2).
(2). .
. (Дж/К).
(Дж/К).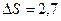 Дж/К.
Дж/К. Дано Решение
Дано Решение м-1 Определять длину волны при всевозможных переходах
м-1 Определять длину волны при всевозможных переходах Бальмера
Бальмера 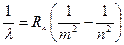 или
или 
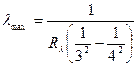 . Минимальное значение длины волны при n → ∞.
. Минимальное значение длины волны при n → ∞. . Вычисления:
. Вычисления:  (м),
(м), (м)
(м) м,
м,  м.
м. Дано Решение
Дано Решение
 (1), где λ – постоянная распада.
(1), где λ – постоянная распада. 
 . Логарифмируем левую и правую части уравнения
. Логарифмируем левую и правую части уравнения  , откуда
, откуда 

 (с) = 10 (мин).
(с) = 10 (мин). может захватывать нейтрон. В результате этого происходит расщепление бора на ядра лития и гелия. Написать ядерную реакцию и определить энергию, освобождающуюся при этой реакции.
может захватывать нейтрон. В результате этого происходит расщепление бора на ядра лития и гелия. Написать ядерную реакцию и определить энергию, освобождающуюся при этой реакции.
 - дефект
- дефект МэВ/а.е.м.
МэВ/а.е.м.
 ? В каждом акте деления выделяется ΔЕ = 200 МэВ энергии.
? В каждом акте деления выделяется ΔЕ = 200 МэВ энергии.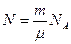 . NA = 6,02·1023 моль-1 –число Авогадро.
. NA = 6,02·1023 моль-1 –число Авогадро. .
.
 .
. .
. , η = 20%.
, η = 20%.


