ГРАФІЧНИЙ МЕТОД
Для визначення центра ваги окремого ходу графічним методом необхідно перенести хід із карти на кальку або накреслити його в масштабі на папері.
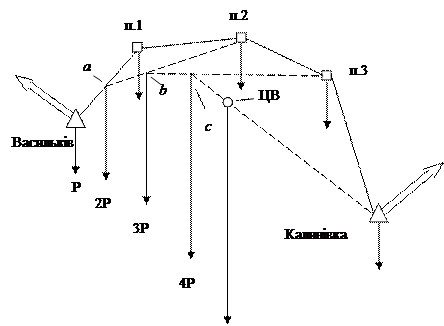
Ріс. 2. Визначення центру ваги ходу графічним методом Використаймо відоме правило механіки про суму паралельних сил. Нехай на пунктах тріангуляції і полігонометрії (рис.2) діють паралельні та однаково направлені сили Р. Тоді результуюча сил в точках Васильків – п.1 дорівнює 2Р, а центр ваги знаходиться в точці а, яка розташована на середині відрізка Васильків – п.1, результуюча сил в точках а – п.2 дорівнює 3Р, центр ваги знаходиться в точці b, яка ділить відрізок а – п.2 у співвідношенні 1:2, що в сумі дорівнює трьом, для напрямку b – п.3 результуюча дорівнює 4Р, а точка с ділить цей відрізок у співвідношенні 1:3, що в сумі дорівнює чотирьом. Центр ваги ходу ЦТ буде знаходитись на відрізку с – Калинівка в точці, яка ділить вказаний відрізок у співвідношенні 1:4.
АНАЛІТИЧНИЙ МЕТОД
Для знаходження центра ваги ходу аналітичним методом необхідно визначити координати його точок в абсолютній або в умовній системі. Для цього в табл. 2 занести номери точок і їх координати X та Y. Координати центра ваги знаходять за формулами:
де nТ – кількість точок в ході, включаючи пункти тріангуляції. Можна провести розрахунки в умовній системі координат. Тоді за початок координат беруть одну з вихідних точок ходу, вісь абсцис спрямовують по замикаючий, а вісь ординат - перпендикулярно до неї. Координати центра ваги в умовній системі знаходять за попередніми формулами з точністю до 10 м. Порівняти результати, отримані різними способами і зробити висновок.
Таблиця 2. Обчислення даних для розрахунку точності окремого полігонометричного ходу
nT = n = Sсер = L = 2a =
7. Визначити форму полігонометричного ходу. Форму ходу необхідно визначити за трьома критеріями. Хід буде витягнутий тоді, коли: а) кут між замикаючою і будь-якою стороною не перевищує 240; б) відношення
де L – довжина замикаючої; Значення S та L визначаються за формулами:
де ΔX, ΔY – різниці координат пунктів ходу, які утворюють довжини S, ΔXП,К, ΔYП,К – різниці координат початкового та кінцевого пунктів ходу; Для контролю необхідно порівняти розрахункові значення S та L з їх графічними аналогами. в) жодна з точок ходу не виходить за межі коридору шириною 2а, що побудований від прямої, проведеної через центр ваги паралельно замикаючій, а=L:8. Межі коридору показати на схемі ходу, де визначено центр ваги. Якщо хоч один критерій вказує на зігнутість ходу, то хід вважається зігнутим. Результати розрахунків занести в табл.2. 8. Прямий розрахунок окремого ходу полігонометрії. В результаті прямого розрахунку ходу визначають очікувану граничну похибку положення точки в слабкому місці. Визначивши форму ходу, підбирають відповідну формулу для розрахунку. Для полігонометричних ходів з наближено рівними сторонами та попереднім зрівноваженням кутів, які спираються на два вихідні пункти з відомими дирекційними кутами, середня квадратична похибка положення кінцевої точки ходу (слабкого місця) дорівнює:
для витягнутого ходу
для зігнутого ходу
де n – число сторін в ході. Якщо довжини ліній полігонометричного ходу вимірювались точними світловіддалемірами, то похибки вимірювань мають випадковий характер і мало залежать від довжини лінії, що дозволяє віднести їх до середньої довжини лінії Sсер. Тоді
де Середня квадратична похибка вимірювання ліній, наприклад, для світловіддалеміра СТ-5 ”Блеск” визначається за формулою:
де Sсер{км} – середня довжина сторони запроектованого ходу в кілометрах,
Середня квадратична похибка вимірювання кутів вибирається з табл.1. Визначення
Значення Після знаходження середньої квадратичної похибки М необхідно перевірити, чи відповідає ця похибка точності запроектованої полігонометрії. Для цього знаходять абсолютну граничну похибку на весь хід:
Знаходять граничну відносну похибку
Відомо, що після прив´язки кінця ходу до кінцевого вихідного пункту завдяки зрівнюванню координат найменшу точність матиме пункт, який розташований в середині ходу – як найбільш віддалений від обох вихідних пунктів [1]. В цьому випадку слабким місцем ходу буде якраз його середина. Тодігранична похибка Δ положення точки полігонометричного ходу (в його середині) після зрівнювання близька до середньої квадратичної похибки М положення кінцевої точки до зрівнювання [1].
Зробити висновок. 9. Зворотній розрахунок окремого ходу. Зворотній розрахунок ніяк не пов’язаний з прямим розрахунком і є самостійним. В результаті зворотного розрахунку знаходять середні квадратичні похибки вимірювання кутів 9.1. Визначити граничну похибку положення точки в середині ходу. Її визначають через граничну відносну похибку 1:Т
На основі принципу рівного впливу кутової та лінійної складових у формулах для визначення М записують для ходу відповідної форми: а) для витягнутого
б) для зігнутого
9.2. Визначити середні квадратичні похибки вимірювання ліній світловіддалеміром і кутів. Із відповідних співвідношень знаходять середні квадратичні похибки вимірювання ліній
а) для витягнутого ходу
б) для зігнутого ходу
9.3. Підбір інструментів. На основі розрахованих значень 9.4 Розрахунок точності центрування теодоліта і марок над пунктами ходу. Середня квадратична похибки
Звідки, використовуючи принцип рівного впливу, визначимо величину одного джерела похибок
Середні квадратичні похибки центрування і редукції дорівнюють
де е, е' – лінійні елементи відповідно центрування і редукції. Тоді
де S – мінімальна довжини сторони ходу.
Знаходять найбільше значення серед е та е' і, орієнтуючись на нього, роблять висновок про метод центрування теодоліта і марок з урахуванням того, що середня квадратична похибка центрування нитяним виском дорівнює 5 мм, а оптичним виском - 1мм. 9.5. Визначити число прийомів вимірювання кутів обраним теодолітом. Для вимірювання кутів на пунктах полігонометрії використовують способи окремого кута та кругових прийомів. Середня квадратична похибка власне вимірювання кута mвв дорівнює
де mвіз, mвід – середні квадратичні похибки відповідно візування на марку та відліку. З урахуванням
отримаємо число прийомів
де mвід =2" – приймається для несприятливих умов освітлення штрихів лімба теодоліта [3], Г =30* - збільшення зорових труб точних оптичних теодолітів. Округлення числа n виконати з надлишком. 10. Розрахунок точності полігонометрії з одною, двома та більше вузловими точками Якщо запроектовано декілька ходів одного розряду, точність розраховують для найбільш довгого хода, а якщо полігонометрична мережа одного розряду запроектована у вигляді системи ходів, мающих одну, або декілька вузлових точок, - то для найбільш складної мережі методом послідовних приближень. Суттєвість метода послідовних приближень заключається в тому, що очікувані помилки знаходження вузлових пунктів вираховують приближенням як середньо вагове із помилок ходів, які сходяться в даному вузловому пункті. В першому наближені система ходів, які сходяться в кожній вузловій точці, розглядається як самостійна система, яка спирається на пункти, помилки в положенні яких рівні нулю. Порядок проведення вирахування для мережі показання на мал.. 3.
Для витягнутого ходу
для зігнутого ходу
де Вираховують середньо квадратичні помилки положення Вираховують вагу вузлового пункту І по ходам 1, 2, 3:
Оскільки в вузлі І сходяться три хода, середня квадратична помилка визначення положення вузлової точки І в першому приближені
де
Аналогічно знаходять очікувану середню квадратичну помилку визначення вузлового пункту ІІ по ходам 3, 4 і 5: Ці розрахунки виконують, припускає, що помилки вихідних даних рівні нулю. В другому приближені пунктах І і ІІ приймають помилки їх визначення, отримані в першому приближені
Аналогічно для пункту ІІ
В третьому наближені в якості помилок вихідних даних приймають помилки положення вузлових пунктів І і ІІ, отриманих в другому приближені, і т. ін. Приближення продовжуються до тіх пір, поки в двох останніх приближеннях будуть отримані практично однакові середньо квадратичні помилки. Обчислення зводять в табл.. 4. Використовуючи отримані середньо квадратичні помилки положення вузлового пункту М, можна отримати середньо квадратичні помилки вимірювання для сторін
Таблиця 4
для витягнутого хода
для зігнутого ходу
Для хода, розміщеного між вузловими точками,
Коротко описати методику світлодальномірних вимірювань, вибрати метод запроектованої геодезичної мережі.
Розраховують середню квадратичну похибку М вузлової точки з кожного ходу, що сходяться в цій точці. Знаходять вагу вузлової точки з ходів №1, №2, №3 за формулою
Оскільки до першої вузлової точки підходять три ходи, то вага цієї точки дорівнює
а її середня квадратична похибка
Аналогічно знаходять очікувану середню квадратичну похибку положення вузлового пункту з ходів №3, №4, №5.
11. Підібрати типи центрів для пунктів полігонометрії. Користуючись інструкціями [2,4], вивчити типи існуючих центрів для закріплення пунктів полігонометрії. Навести креслення центрів У15, У15н, У15к та стінного знаку закріплення полігонометричного центра (тип 143). Вибрати типи центрів та вказати їх в табл.2. 12. Навести схеми закріплення пунктів полігонометрії стінними знаками. Приводять типові схеми закріплення пунктів полігонометрії стінними відновлювальними та орієнтирними знаками [3]. Коротко описують переваги та недоліки кожного типу знаків, процес закріплення. 13. Скласти картку закладки одного пункту полігонометрії. В картці закладки пункту полігонометрії (кроки пункту полігонометрії) накреслити пункт полігонометрії та ситуацію, що його оточує, показати прив´язку пункту до місцевих предметів, зробити короткий опис його місцезнаходження, вказати тип центра, його номер та виконавців робіт (додаток 2) [2]. 14. Кожен студент виконує індивідуальне завдання. Обсяг курсового проекту: проект полігонометрії на кальці та пояснювальна записка – 20…30 сторінок.
Література: 1. Селиханович В.Г. Геодезия. –М.: Недра, 1981. 2. Інструкція з топографічного знімання у масштабах 1:5000, 1:2000, 1:1000 та 1:500. ГКНТА – 2.04 – 02 – 98, Київ.: ГУГК та К, 1992. 3. Тревого И.С., Шевчук М.П. Городская полігонометрія. М.: Недра, 1986. 4. Інструкція. Про типи центрів геодезичних пунктів. ГКНТА – 2.01, 02 – 01 – 93. – Київ.: ГУГК та К, 1994. 5. Таблицы для вычисления прямоугольных координат улов рамок трапеции в проекции Гаусса – Крюгера на эллипсоиде Красовського. М.: ГУГК, 1948. 6. Большая Советская Энциклопедия. М.:1977. 7. Проектування й розрахунок полігонометрії згущення. Методичні рекомендації до виконання курсового проекту з дисципліни “Геодезія” для студентів спеціальностей 7.070901 “Геодезія” та 7.070904 “Землевпорядкування та кадастр”. Укл. Г.М.Литвин, О.П.Каєв. – Київ: КДТУБА, 1998. 8. Геодезія. Частина перша. Під ред. Могильного С.Г. і Войтенко С.П. – Чернігів, КП “Чернігівські обереги”, 2002р.
|



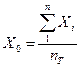 ,
,
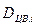 ,
км
,
км
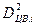 , км2
, км2

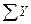
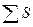

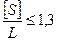 ,
, – сума довжин сторін ходу,
– сума довжин сторін ходу,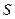 =
=  ;
; =
=  ,
,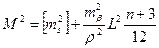 ;
;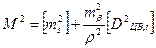 ;
;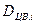 – відстань від центру ваги до кожної точки ходу,
– відстань від центру ваги до кожної точки ходу,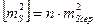 ,
,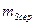 - середня квадратична похибка вимірювання.
- середня квадратична похибка вимірювання.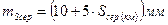 ,
,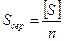
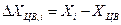 ,
, ,
, .
.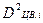 та
та  [
[ 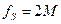
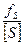 та порівнюють її з граничною відносною похибкою ходу для полігонометрії 4 класу
та порівнюють її з граничною відносною похибкою ходу для полігонометрії 4 класу 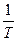 (див табл.1). Повинна виконуватись умова
(див табл.1). Повинна виконуватись умова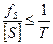 .
.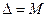
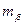 і ліній
і ліній 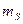 запроектованого ходу, користуючись якими підбирають типи кутомірних приладів і світловіддалемірів. Розрахунок ведуть згідно граничної похибки ходу 1:Т в такій послідовності:
запроектованого ходу, користуючись якими підбирають типи кутомірних приладів і світловіддалемірів. Розрахунок ведуть згідно граничної похибки ходу 1:Т в такій послідовності: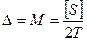 .
.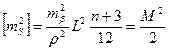 ,
,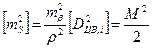 ,
,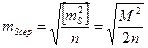 ,
,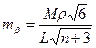 ,
,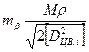 .
.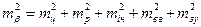 .
.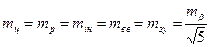 .
.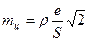 ,
,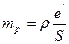 ,
,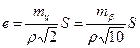 ,
,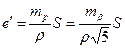 ,
,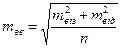 ,
, ,
,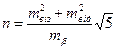 ,
, ,
, ;
;
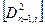 - сума відстаней від кожної точки хода (вузлової точки) до всіх кутів повороту хода (включаючи початковий східний пункт).
- сума відстаней від кожної точки хода (вузлової точки) до всіх кутів повороту хода (включаючи початковий східний пункт).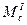 вузлового пункту І по кожному ходу, с ходячому в цьому пункті.
вузлового пункту І по кожному ходу, с ходячому в цьому пункті.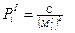 .
.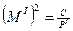 ,
,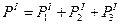 .
.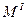 і
і 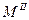 за помилками вихідних даних. Тоді для пункту І
за помилками вихідних даних. Тоді для пункту І ;
; 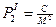 ;
; 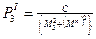 .
.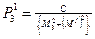 ;
; 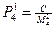 ;
; 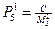 .
.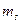 і кутів
і кутів 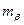 для кожного із ходів, примыкающих до данного пункту:
для кожного із ходів, примыкающих до данного пункту: ;
;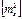

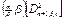
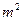
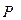
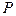

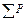
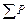

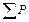
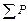
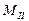
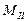
 ;
;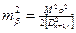 .
.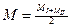 .
.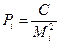 .
.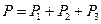 ,
,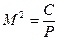 .
.


