Модели линейных систем
1. Заварыкин В.М., Житомирский В.Г., Лапчик М.П. Численные методы. М.: Просвещение. – 1991. – 175с. 2. Ракитин В.И., Первушин В.Е. Практическое руководство по методам вычислений. М.: Высшая школа. – 1998. 384с. 3. Волков Е.А. Численные методы. М.: Наука. – 1987. – 248 с. 3. Турчак Л.И. Основы численных методов. М.: Наука. – 1987. – 318с. 4. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. М.: Наука. – 1972. – 366с. 5. Березин И.С., Жидков Н.П. Методы вычислений. Т.1. М.: Наука. – 1966. – 632с. 6. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М. – С.П.: Физматлит. – 2001. – 630с. 7. С. Ф. Аминова, Р. М. Асадуллин. Лабораторный практикум по курсу «Численные методы».- Уфа: Изд-во БГПУ, 2003 –28с. 8. Р. Р. Сулейманов. Решение математических задач в системе MathCAD 8.1 // Учитель Башкортостана. 2002. № 2. 10. MATHCAD 6.0 PLUS/ Финансовые, инженерные и научные расчеты в среде Windows 95./ Пер. с англ. – М.: Информационно-издательский дом "Филинъ", 1996. – 712 с. 11. Плис А.И., Сливина Н.А. Mathcad: математический практикум. – М.: Финансы и Статистика. – 1999. 12. Очков В.Ф. Mathcad 8 Pro для студентов и инженеров. – М.: КомпьютерПресс, 1999. 13. Очков В.Ф.. MathCad 7 Pro для студентов и инженеров. – М.: КомпьютерПресс, 1998. – 384 с. 14. Дьяконов В.П. Справочник по MathCAD PLUS 6.0 PRO. – М.: CK Пресс, 1997. – 336 с.
К. Поляков Исследование САУ с помощью среды Matlab ©, 2004-2005 Исследование САУ при случайных возмущениях с помощью среды Matlab ©, 2009 Методические указания к выполнению лабораторных работ Лабораторная работа № 1 Исследование разомкнутой линейной системы Цели работы · освоение методов анализа одномерной линейной непрерывной системы с помощью среды Matlab Задачи работы · ввести модель системы в виде передаточной функции · построить эквивалентные модели в пространстве состояний и в форме «нули-полюса» · определить коэффициент усиления в установившемся режиме и полосу пропускания системы · научиться строить импульсную и переходную характеристики, карту расположения нулей и полюсов, частотную характеристику · научиться использовать окно LTIViewer для построения различных характеристик · научиться строить процессы на выходе линейной системы при произвольном входном сигнале Краткие теоретические сведения Модели линейных систем Для описания линейных систем могут применяться несколько способов: · дифференциальные уравнения · модели в пространстве состояний · передаточные функции · модели вида «нули-полюса» Первые два способа называются времен ы ми, поскольку описывают поведение системы во временной области и отражают внутренние связи между сигналами. Передаточные функции и модели вида «нули-полюса» относятся к частотным способам описания, так как непосредственно связаны с частотными характеристиками системы и отражают только вход-выходные свойства (то есть, описывают динамику не полностью). Частотные методы позволяют применять для анализа и синтеза алгебраические методы, что часто упрощает расчеты. С другой стороны, для автоматических вычислений более пригодны методы, основанные на моделях в пространстве состояний, поскольку они используют вычислительно устойчивые алгоритмы линейной алгебры. Исходные уравнения динамики объектов, которые строятся на основе законов физики, имеют вид нелинейных дифференциальных уравнений. Для приближенного анализа и синтеза обычно проводят их линеаризацию в окрестности установившегося режима и получают линейные дифференциальные уравнения. Линейное уравнение
Передаточная функция Передаточная функция звена, которое описывается приведенным выше уравнением, равна
то есть, совпадает с отношением операторных полиномов Передаточная функция в среде Matlab вводится в виде отношения двух многочленов (полиномов) от комплексной переменной s. Полиномы хранятся как массивы коэффициентов, записанных по убыванию степеней. Например, передаточная функция >> n = [2 4] n = 2 4 >> d = [1 1.5 1.5 1] d = 1.0000 1.5000 1.5000 1.0000 >> f = tf (n, d) Transfer function: 2 s + 4 ------------------------- s^3 + 1.5 s^2 + 1.5 s + 1 или сразу, без предварительного построения числителя и знаменателя: >> f = tf ([2 4], [1 1.5 1.5 1]); В памяти создается объект класса tf, описывающий передаточную функцию. Точка с запятой в конце команды подавляет вывод на экран. По передаточной функции можно легко построить модель в форме «нули-полюса» >> f_zpk = zpk(f) Zero/pole/gain: 2 (s+2) ----------------------- (s+1) (s^2 + 0.5s + 1) Нулями называются корни числителя, полюсами – корни знаменателя. Эта функция имеет один нуль в точке Модель в пространстве состояний связана с записью дифференциальных уравнений в стандартной форме Коши (в виде системы уравнений первого порядка):
Здесь Для преобразования передаточной функции в модель в пространстве состояний используется команда >> f_ss = ss (f) a = x1 x2 x3 x1 -1.5 -0.1875 -0.03125 x2 8 0 0 x3 0 4 0 b = u1 x1 0.5 x2 0 x3 0 c = x1 x2 x3 y1 0 0.5 0.25 d = u1 y1 0 Это означает, что матрицы модели имеют вид
Модель в пространстве состояний можно построить не для всех передаточных функций, а только для правильных, у которых степень числителя не выше, чем степень знаменателя. Например, передаточная функция Используют также понятие строго правильной функции, у которой степень числителя меньше, чем степень знаменателя. Если построить модель в пространстве состояний для такой функции, матрица
|

 можно записать в операторной форме
можно записать в операторной форме или
или  , где
, где  – входной сигнал,
– входной сигнал, 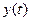 – сигнал выхода,
– сигнал выхода, 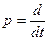 – оператор дифференцирования,
– оператор дифференцирования, 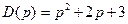 и
и 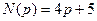 – операторные полиномы.
– операторные полиномы. линейной стационарной системы от комплексной переменной
линейной стационарной системы от комплексной переменной  определяется как отношение преобразования Лапласа выхода к преобразованию Лапласа входа при нулевых начальных условиях
определяется как отношение преобразования Лапласа выхода к преобразованию Лапласа входа при нулевых начальных условиях 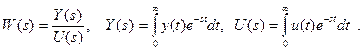
 ,
, при замене переменной
при замене переменной  на
на  вводится следующим образом[1]
вводится следующим образом[1] и три полюса в точках
и три полюса в точках  и
и  . Паре комплексных полюсов соответствует квадратный трехчлен.
. Паре комплексных полюсов соответствует квадратный трехчлен.
 – вектор переменных состояния размера
– вектор переменных состояния размера  ,
, 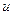 – вектор входных сигналов (вектор управления) размера
– вектор входных сигналов (вектор управления) размера  и
и  – вектор выходных сигналов размера
– вектор выходных сигналов размера  . Кроме того,
. Кроме того,  и
и  – постоянные матрицы. Согласно правилам матричных вычислений, матрица
– постоянные матрицы. Согласно правилам матричных вычислений, матрица  должна быть квадратной размера
должна быть квадратной размера  , матрица
, матрица  имеет размер
имеет размер 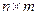 , матрица
, матрица  –
– 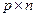 и матрица
и матрица  . Для систем с одним входом и одним выходом[2] матрица
. Для систем с одним входом и одним выходом[2] матрица  ,
,  ,
,  ,
,  .
. – неправильная, она не может быть преобразована в модель в пространстве состояний.
– неправильная, она не может быть преобразована в модель в пространстве состояний.


