Частотная характеристика
При подаче на вход линейной системы гармонического (синусоидального) сигнала Частотная характеристика определяется как реакция системы на комплексный экспоненциальный сигнал Зависимость модуля величины АЧХ показывает, насколько усиливается амплитуда сигналов разных частот после прохождения через систему, а ФЧХ характеризует сдвиг фазы сигнала.
Реальные объекты имеют строго правильную передаточную функцию, поэтому их АЧХ убывает с ростом частоты и асимптотически стремится к нулю. Говорят, что такой объект обладает свойством фильтра – фильтрует (не пропускает) высокочастотные сигналы (помехи, шумы измерений). Это свойство служит основой для использования метода гармонического баланса. Частота, после которой значение АЧХ уменьшается ниже 0 дБ (коэффициент усиления меньше 1, сигнал ослабляется), называется частотой среза системы >> b = bandwidth (f) Максимум АЧХ соответствует частоте, на которой усиление наибольшее. Значение АЧХ при Для систем с интегрирующими звеньями частотная характеристика стремится к бесконечности при Чтобы построить частотные характеристики в Matlab, надо сначала создать массив частот в нужном диапазоне. Для этого можно использовать функции linspace (равномерное распределение точек по линейной шкале) и logspace (равномерное распределение точек по логарифмической шкале). Команда >> w = linspace (0, 10, 100);строит массив из 100 точек с равномерным шагом в интервале от 0 до 10, а команда >> w = logspace (-1, 2, 100);– массив из 100 точек с равномерным шагом по логарифмической шкале в интервале от Частотная характеристика на сетке w для линейной модели f (заданной как передаточная функция, модель в пространстве состояний или в форме «нули-полюса») вычисляется с помощью функции freqresp: >> r = freqresp(f, w); Функция freqresp возвращает трехмерный массив. Это связано с тем, что она применима и для многомерных моделей (с несколькими входами и выходами), передаточная функция которых представляет собой матрицу. Первые два индекса обозначают строку и столбец в этой матрице, а третий – номер точки частотной характеристики. Для системы с одним входом и одним выходом удобно преобразовать трехмерный массив в одномерный командой >> r = r(:); Для вывода графика АЧХ на экран можно использовать команды Matlab >> plot (w, abs(r)); >> semilogx (w, abs(r)); >> loglog (w, abs(r)); В первом случае масштаб обеих осей координат – линейный, во втором случае используется логарифмический масштаб по оси абсцисс (частот), в последнем – логарифмический масштаб по обеим осям. Для вычисления фазы (в градусах) используется команда >> phi = angle(r)*180/pi; после чего можно строить ФЧХ, например: >> semilogx (w, phi);
|

 с частотой
с частотой  (она измеряется в радианах в секунду), на выходе будет также гармонический сигнал той же частоты, но другой амплитуды и фазы[4]
(она измеряется в радианах в секунду), на выходе будет также гармонический сигнал той же частоты, но другой амплитуды и фазы[4] 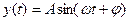 , где
, где  – амплитуда и
– амплитуда и 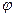 – сдвиг фазы.
– сдвиг фазы.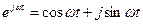 . Для ее построения надо использовать подстановку
. Для ее построения надо использовать подстановку  в передаточной функции
в передаточной функции  . Выражение
. Выражение  называется частотной передаточной функцией или амплитудно-фазовой частотной характеристикой системы (АФЧХ).
называется частотной передаточной функцией или амплитудно-фазовой частотной характеристикой системы (АФЧХ).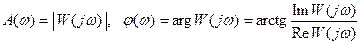 .
.

 .Частота, после которой значение АЧХ падает ниже -3 дБ (коэффициент усиления меньше, чем 0.708), называется полосой пропускания системы
.Частота, после которой значение АЧХ падает ниже -3 дБ (коэффициент усиления меньше, чем 0.708), называется полосой пропускания системы  . Для ее вычисления используют команду
. Для ее вычисления используют команду равно усилению при постоянном сигнале, то есть, статическому коэффициенту усиления
равно усилению при постоянном сигнале, то есть, статическому коэффициенту усиления 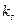 . Это следует и из равенства
. Это следует и из равенства  .
. . Это значит, что их выход бесконечно увеличивается или уменьшается при постоянном входном сигнале.
. Это значит, что их выход бесконечно увеличивается или уменьшается при постоянном входном сигнале. до
до  .
.


