Переходной характеристикой (переходной функцией) 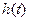 называется реакция системы (при нулевых начальных условиях) на единичный ступенчатый сигнал (единичный скачок)
называется реакция системы (при нулевых начальных условиях) на единичный ступенчатый сигнал (единичный скачок)

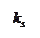
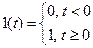 .
.
Импульсная и переходная функции связаны выражениями
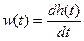 ,
, 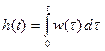 .
.
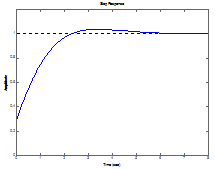 Для систем без интеграторов переходная характеристика стремится к постоянному значению. Переходная характеристика системы с дифференцирующим звеном (числитель передаточной функции имеет нуль в точке
Для систем без интеграторов переходная характеристика стремится к постоянному значению. Переходная характеристика системы с дифференцирующим звеном (числитель передаточной функции имеет нуль в точке  ) стремится к нулю. Если система содержит интегрирующие звенья, переходная характеристика асимптотически стремится к прямой, параболе и т.д., в зависимости от количества интеграторов.
) стремится к нулю. Если система содержит интегрирующие звенья, переходная характеристика асимптотически стремится к прямой, параболе и т.д., в зависимости от количества интеграторов.
По определению предельное значение переходной функции 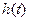 при
при 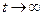 есть статический коэффициент усиления:
есть статический коэффициент усиления: 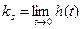 .
.
Эта величина имеет смысл только для устойчивых систем, поскольку при неустойчивости переходный процесс не сходится к конечному значению.
 Если передаточная функция правильная, но не строго правильная (матрица
Если передаточная функция правильная, но не строго правильная (матрица  модели в пространстве состояний не равна нулю), скачкообразное изменение входного сигнала мгновенно приводит к скачкообразному изменению выхода. Величина этого скачка равна отношению коэффициентов при старших степенях числителя и знаменателя передаточной функции (или матрице
модели в пространстве состояний не равна нулю), скачкообразное изменение входного сигнала мгновенно приводит к скачкообразному изменению выхода. Величина этого скачка равна отношению коэффициентов при старших степенях числителя и знаменателя передаточной функции (или матрице  модели в пространстве состояний).
модели в пространстве состояний).
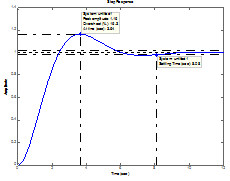
По переходной характеристике можно найти важнейшие показатели качества системы – перерегулирование (overshoot) и время переходного процесса (settling time).
Перерегулирование определяется как 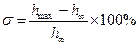 ,
,
где 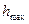 – максимальное значение функции
– максимальное значение функции 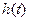 , а
, а 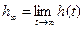 – установившееся значение выхода.
– установившееся значение выхода.
Время переходного процесса – это время, после которого сигнал выхода отличается от установившегося значения не более, чем на заданную малую величину (в среде Matlab по умолчанию используется точность 2%).

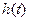 называется реакция системы (при нулевых начальных условиях) на единичный ступенчатый сигнал (единичный скачок)
называется реакция системы (при нулевых начальных условиях) на единичный ступенчатый сигнал (единичный скачок)
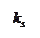
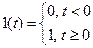 .
.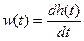 ,
, 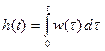 .
. Для систем без интеграторов переходная характеристика стремится к постоянному значению. Переходная характеристика системы с дифференцирующим звеном (числитель передаточной функции имеет нуль в точке
Для систем без интеграторов переходная характеристика стремится к постоянному значению. Переходная характеристика системы с дифференцирующим звеном (числитель передаточной функции имеет нуль в точке  ) стремится к нулю. Если система содержит интегрирующие звенья, переходная характеристика асимптотически стремится к прямой, параболе и т.д., в зависимости от количества интеграторов.
) стремится к нулю. Если система содержит интегрирующие звенья, переходная характеристика асимптотически стремится к прямой, параболе и т.д., в зависимости от количества интеграторов.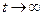 есть статический коэффициент усиления:
есть статический коэффициент усиления: 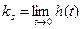 .
. Если передаточная функция правильная, но не строго правильная (матрица
Если передаточная функция правильная, но не строго правильная (матрица  модели в пространстве состояний не равна нулю), скачкообразное изменение входного сигнала мгновенно приводит к скачкообразному изменению выхода. Величина этого скачка равна отношению коэффициентов при старших степенях числителя и знаменателя передаточной функции (или матрице
модели в пространстве состояний не равна нулю), скачкообразное изменение входного сигнала мгновенно приводит к скачкообразному изменению выхода. Величина этого скачка равна отношению коэффициентов при старших степенях числителя и знаменателя передаточной функции (или матрице 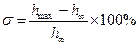 ,
,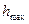 – максимальное значение функции
– максимальное значение функции 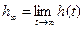 – установившееся значение выхода.
– установившееся значение выхода.


