| Этап выполнения задания
| Команды Matlab
|
| 1. Сделайте свою папку рабочей папкой Matlab.
| ЛКМ по кнопке  справа от поля Current Directory справа от поля Current Directory
|
| 2. Откройте окно рабочей папки.
| View – Current directory
|
| 3. Откройте модель, построенную в лабораторной работе № 4.
| двойной щелчок на lab4.mdl
|
| 4. Сохраните модель в своей папке под именем lab5.mdl.
|  File – Save as... File – Save as...
|
| 5. Удалите модель линейной системы, оба мультиплексора и лишние соединительные линии. Достройте схему, как показано на рисунке.
| 
|
| 6. Замените числовые значения постоянного возмущения и заданного курса на символьные: fConst и phiZad соответственно.
|  Двойной щелчок на блоке
Final value
Двойной щелчок на блоке
Final value
|
7. Откройте блок Нелинейная система и замените все числовые значения на имена переменных во всех подсистемах. Через deltaMax обозначим максимальный угол перекладки руля ( ), а через ddMax – максимальную скорость перекладки ( ), а через ddMax – максимальную скорость перекладки ( ). ).
| Судно, Numerator: K
Denominator: [Ts 1 0]
ПД-регулятор:Numerator: Kc*[Ts+1 1]
И-канал, Denominator: [TI 0]
Гирокомпас, Denominator: [Toc 1]
Привод, Denominator: [TR 0]
Ограничение скорости перекладки руля: ±TR*ddMax
Ограничение угла перекладки руля: ±deltaMax
|
| 8. Объясните, почему введены именно такие параметры для ПД-регулятора и для блока ограничения угла перекладки руля.
|
| 9. Вставьте в отчет схемы всех подсистем нелинейной модели. После этого закройте все окна подсистем, кроме главного окна модели.
|
| 10. Перейдите в командное окно Matlab и создайте новый М-файл.
| File – New – M-file
|
| 11. Введите численные значения всех параметров модели для своего варианта. Установите заданный курс 30 градусов. Сохраните файл под именем sysdata.m.
| clear all;
clc;
K = 0.0694; Ts = 18.2;
TR = 2; Toc = 6;
ddMax = 3; deltaMax = 30;
phiZad = 30; fConst = 0;
TI = 200; Kc = 0.7045;
|
| 12. Выполните скрипт, после этого запустите модель. Добейтесь, чтобы моделирование было успешно выполнено. Если этого не происходит, сообщения об ошибках надо искать в командном окне Matlab.
| клавиша F5
 ЛКМ по кнопке ЛКМ по кнопке 
|
| 13. Откройте в редакторе скрипт lab4graph.m и сохраните его под именем lab5graph.m.
| двойной щелчок на lab4graph.m
File – Save as...
|
| 14. Добавьте в начало скрипта строку, показанную справа. При этом скрипт становится функцией, принимающей два массива – phi и delta. Эта функция ничего не возвращает, а только строит график в отдельном окне. Она имеет собственное пространство переменных и не может (без специальных приемов) использо-вать переменные рабочей области Matlab.
| function lab5graph (phi, delta)
|
| 15. Удалите из функции лишние строки, учитывая, что теперь массивы phi и delta имеют только 2 столбца (строятся только процессы в нелинейной системе).
|
| 16. Измените заголовок на «Переходные процессы при изменении курса». Сохраните файл и скопируйте текст функции в отчет.
| title (...)
|
| 17. Создайте новый М-файл, введите в первой строчке вызов скрипта sysdata (загрузка параметров модели). Добавьте строки для запуска моделирования (модель lab5.mdl) и вывода результатов на экран. Сохраните скрипт под именем lab5go.m и скопируйте его в отчет.
| sysdata;
sim ('lab5')
lab5graph (phi, delta)
|
| 18. Теперь построим функцию, которая вычисляет перерегулирование и время переходного процесса. Создайте новый М-файл в редакторе и введите в него текст функции[26]:
1 function [sigma,Tpp] = overshoot (t, y)
2 yInf = y(end);
3 diff = (y - yInf) / abs (yInf);
4 sigma = max(diff) * 100;
5 i = find(abs(diff) > 0.02);
6 Tpp = t(max(i)+1);
Комментарий:
1 – объявление функции overshoot, которая принимает два параметра-массива (время t и переходный процесс y) и возвращает два значения (перерегулирование в процентах sigma и время переходного процесса Tpp).
2 – вычисление последнего значения массива y, которое принимается за установившееся значение
3 – вычисление относительного отклонения в каждой точке графика
4 – вычисление перерегулирования в процентах
5 – в массив i записываются номера всех элементов массива diff, которые по модулю больше 0.02 (для определения времени переходного процесса используется отклонение 2%)
6 – вычисляется время переходного процесса как первый элемент массива t, после которого все элементы массива y отклоняются от установившегося значения не более, чем на 2%.
|
| 19. Сохраните файл с именем overshoot.m и скопируйте его в отчет.
|
20. Перейдите в окно скрипта lab5go. Удалите последние две строчки, оставив только загрузку исходных данных. Сохраните файл с именем lab5go1.m. В последней части работы мы исследуем влияние параметров модели на показатели качества переходных процессов. Сначала посмотрим, как влияет постоянная времени судна 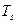 [27]. [27].
|
| 21. Добавьте в конец скрипта текст программы (без номеров строк)
1 Ts0 = Ts;
2 aTs = linspace(0.8, 1.2, 100) * Ts0;
3 aSi = []; aTpp = [];
4 for Ts=aTs
5 sim ('lab5')
6 [si,Tpp] = overshoot (phi(:,1), phi(:,2));
7 aSi = [aSi si];
8 aTpp = [aTpp Tpp];
9 end;
Комментарий:
1 – сохраняем номинальное значение постоянной времени в переменной Ts0
2 – создается массив из 100 постоянных времени, которые изменяются в диапазоне от 80 до 120% от номинального (расчетного) значения
3 – создаются пустые массивы aSi (для хранения значений перерегулирования) и aTpp (для хранения значений времени переходного процесса)
4 – начало цикла, переменная Ts принимает последовательно все значения из массива aTs
5 – моделирование при новом значении Ts
6 – вычисление перерегулирования и времени переходного процесса
7 – в конец массива aSi добавляется новое значение
8 – в конец массива aTpp добавляется новое значение
9 – конец цикла
|
| 22. Чтобы регулятор не изменялся при изменении Ts, необходимо в модели изменить в его числителе Ts на Ts0.
| ПД-регулятор:
Numerator: Kc*[Ts0+1 1]
|
| 23. Запустите скрипт на выполнение. Если открыть окно осциллографа Курс, можно наблюдать, как изменяется переходный процесс при изменении постоянной времени.
| клавиша F5
|
| 24. Добавьте в конец скрипта строки для построения графика. В верхней части надо построить график изменения перерегулирования, в нижней – изменение времени переходного процесса, Здесь удобно использовать элементы из файла lab5graph.m, исправив их соответствующим образом.
|
| 25. Сохраните скрипт и запустите на выполнение только новые строки. Чтобы не проводить моделирование заново, можно выделить их в редакторе и нажать F9. Скопируйте отлаженный скрипт в отчет.
| выделить строки, клавиша F9
|
| 26. Если график изменения времени переходного процесса имеет ступенчатый или скачкообразный характер, уменьшите максимально допустимый шаг интегрирования и повторите моделирование (учтите, что время выполнения скрипта увеличится).
|  Simulation –
Simulation parameters –
Max step size = 0.2
Simulation –
Simulation parameters –
Max step size = 0.2
|
| 27. Скопируйте полученный график в отчет.
|
| 28. Сохраните скрипт с именем lab5go2.m. Исправьте его так, чтобы исследовать зависимости показателей качества от угла поворота судна от 1 до 110 градусов с шагом 1 градус.
|
| 29. Скопируйте отлаженный скрипт и полученный график в отчет. Объясните полученные кривые. Как они должны были бы выглядеть для линейной системы?
|
1. В параметрах блока модели указано имя переменной. Как задать ее значение?
2. Как ввести ограничение на скорость перекладки руля, если известна постоянная времени привода?
3. Что такое М-файл?
4. Как создать новый М-файл?
5. Где выводятся сообщения об ошибках при выполнении скрипта или функции?
6. Как строится заголовок функции в М-файле?
7. Может ли функция возвращать несколько величин?
8. Можно ли обращаться к переменным рабочей области Matlab внутри функции?
9. Как вызывается функция, записанная в М-файл?
10. Как выделить последний элемент массива?
11. Чему равен результат операции A-x, где A – массив, а x – число?
12. Как работает функция find?
13. Как изменить функцию overshoot, чтобы она определяла время переходного процесса с точностью 5%?
14. Что такое грубость (робастность) системы?
15. Что означает запись
16. Как выполнить только несколько строк из скрипта?

 справа от поля Current Directory
справа от поля Current Directory
 File – Save as...
File – Save as...

 ), а через ddMax – максимальную скорость перекладки (
), а через ddMax – максимальную скорость перекладки ( ).
).

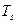 [27].
[27].
 ,рад/сек
,рад/сек
 , сек
, сек
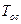 , сек
, сек



