ВИЗНАЧЕННЯ КОЕФІЦІЄНТА ОПОРУ ТЕРТЯ ПО ДОВЖИНІ ТРУБОПРОВОДУ.
Мета роботи: Уяснити фізику природи гідравлічних втрат на основі експериментальних замірів коефіцієнту гідравлічного опору тертя (коефіцієнт Дарсі) і порівняти його з обчисленим по емпіричних формулах з довідників значеннями, або взятими з діаграми.
Загальні відомості При русі реальної рідини виникають сили опору. На їх.подолання затрачається частина енергії, якою володіє рухома рідина. Втрати напору складаються з втрат по довжині і місцевих втрат
Втрати енергії (напору) по довжині
де
Коефіцієнт
При ламінарному режимі втрати пропорційні швидкості в першому ступені 2. Друга область – перехідна і знаходиться приблизно у діапазоні 2000 < Rе < 3000. значення коефіцієнта λ у цій зоні можна визначити тільки наближено по формулі із сусідніх зон. Всі інші області опору знаходяться в зоні турбулентного режиму руху. При турбулентному, що характеризується хаотичним рухом часток рідини, у стінок труби зберігається тонкий шар рідини, де частки рухаються шарами: так званий ламінарний підшар. (Товщина в’язкого підшару
При турбулентному режимі руху виділяють три області опору: 3. Область гідравлічно гладких труб. Труби вважаються гідравлічно гладкими, якщо товщина ламінарного підшару
або (при числах
Використовуючи цей вираз для
Порівняння з ламінарним режимом показує, що при переході до турбулентного режиму вплив в'язкості на опір значно зменшується і, навпаки, значно зростає вплив швидкості руху рідини. Це зумовлюється тим, що в турбулентному потоці в’язкісний опір зосереджений лише в межах тонкого шару у стінок. Основна частина опору створюється за рахунок змішування часток у турбулентному ядрі з розсіюванням кінематичної енергії обертання завихрених часточок. 4. Область перехідна від області гідравлічно гладких труб до квадратичної. Ця область відповідає значенням числа Рейнольдса:
Тут товщина в’язкого підшару Для визначення коефіцієнта Френзеля
Кольбрука–Уайта
або Альтшуля
5. Область розвинутого турбулентного потоку, чи квадратичного опору. Величина
При великих числах Рейнольдса товщина в’язкого підшару стає настільки мала ( Коефіцієнт Нікурадзе
Шифрінсона
Слід зауважити, що ступінь впливу шорсткості на потік залежить не тільки від середньої висоти виступів, але також від їхньої форми й положення. Середнє значення еквівалентної шорсткості
Опис лабораторної установки Схема установки приведена на рис.2.3.1. Установка складається з нижнього баку 14, що служить одночасно основою установки, напірного резервуара 3, панелі п’єзометричних трубок 7 і досліджуваних ділянок труб 8 і 9 і мірного бачка 16.
А
Б Рис. 2.3.1. Лабораторна установка для вивчення гідравлічного опору а – вид спереду; б – принципова схема; 1 – насос; 2 – напірний трубопровід; 3, 14, 16 –бак; 4, 12 – переливна труба; 5 – вмикач; 6 – індикаторна лампа; 7 – п’єзометри; 8,9 – експериментальний трубопровід; 10 – термометр; 13 – вимірювальне скло,15. – індикаторне скло наявності достатньої кількості води.
В середині бака встановлений насос 1. На передній панелі розміщені маховички керування краном підведення 18, краном зливу з мірного бачка 17 і краном зливу води з досліджуваної труби 11. Мірний бачок 16 має переливну трубу 12, що не допускає його переповнення. Робочий рівень у мірному бачку контролюється візуально по шкалі 13. При роботі насоса 1 вода по трубопроводу 2, регульованому краном 18, подається в напірний бак 3. Постійний рівень у напірному баці підтримується за допомогою зливної труби 4. На цій установці досліджуються втрати напору по довжині труби 8, а також в місцевих опорах на ділянці трубопроводу 9 з місцевими опорами. Порядок виконання роботи Студент перед початком роботи повинен ознайомитися з установкою і замалювати її схему в лабораторному журналі. Визначити розміри дослідної ділянки труби. Запустити насос і наповнити напірний бак. При закритому крані 11 перевіряють роботу п’єзометрів. При відсутності повітря в п’єзометрах і з'єднувальних трубках рівні в них установлюються однакові. Якщо не однакові – прочистити трубки. Потім поступово відкривають кран 11 і після встановлення певної витрати знімають показання п’єзометрів, встановлених у кінці вимірюваної ділянки. Визначають об'ємним способом по мірному бачку витрату, що проходить по трубопроводу. Потім збільшують витрату і роблять усі вище зазначені виміри. Так роблять 4-5 замірів. Виміряти в кожному досліді температуру води. Результати дослідів заносять в табл. 2.3.1. Після проведення дослідів вимикають насос. Витрату, що проходить по трубопроводу, можна визначити і за допомогою діафрагми, якщо вона вмонтована в трубопровід. Для визначення витрати за допомогою діафрагми необхідно виміряти перепад тисків перед і за діафрагмою,
де Обробка дослідних даних 1. Втрати напору на ділянці трубопроводу визначають по різниці показання п’єзометрів
де 2. Витрата води визначається по формулі
S м. б- площа мірного баку; Т – час. 3. Площа мірного бака S м. б . = 30,7x12,5 см2. 4. Середня швидкість руху рідини в трубопроводі дорівнює
де Результати обробки заносять у таблицю 2.3.1.
Таблиця 2.3.1. Експериментальні й обчислені значення
5. Визначити число Рейнольдса
де 6. Визначити коефіцієнт Дарси
і порівняти його з отриманим Підрахувати розбіжності в відсотках між експериментальними
7. Визначається область опору для кожного досліду і за одною вказаною вище формул визначається
За отриманими даними побудувати графік Контрольні запитання 1.Від чого залежить товщина ламінарного підшару? 2. Назвіть області опорів для турбулентного режиму руху рідини? 3. По якій формулі можна визначити втрати напору для ламінарного руху рідини? 4. Напишіть формули для визначення коефіцієнта втрат по довжині для турбулентного руху. 5. Від чого залежить коефіцієнт Дарсі 6. Чим обумовлені втрати напору по довжині трубопроводу? 7. Чи може збільшуватись гідравлічний опір при зменшенні коефіцієнта в’язкості? 8. Як зміниться гідравлічний опір при ламінарному русі рідини, і за рахунок охолодження, зменшення коефіцієнта в’язкості в два рази? 9. Як зміниться гідравлічний опір при розвинутому турбулентному русі і зменшенню коефіцієнта в’язкості в два рази, наприклад, за рахунок нагрівання? 10. Як зміняться втрати напору при турбулентному русі, якщо потрібно подати ту ж витрату по трубах в два рази меншого діаметру?
|

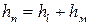
 при русі в’язкої рідини в напірному трубопроводі визначаються по формулі Дарсі - Вейсбаха
при русі в’язкої рідини в напірному трубопроводі визначаються по формулі Дарсі - Вейсбаха (3.1)
(3.1) – коефіцієнт опору тертя по довжині (коефіцієнт Дарсі);
– коефіцієнт опору тертя по довжині (коефіцієнт Дарсі); – довжина і діаметр трубопроводу;
– довжина і діаметр трубопроводу;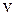 – середня швидкість.
– середня швидкість. , а в іншому діапазоні - переважний вплив роблять геометричні характеристики: відносна шорсткість (відношення висоти бугорків шорсткості
, а в іншому діапазоні - переважний вплив роблять геометричні характеристики: відносна шорсткість (відношення висоти бугорків шорсткості  ) до діаметру труби. У зв'язку з цим розрізняють п’ять областей опору. 1.Перша область – ламінарного руху рідини. Вона обмежується значеннями чисел Рейнольдса
) до діаметру труби. У зв'язку з цим розрізняють п’ять областей опору. 1.Перша область – ламінарного руху рідини. Вона обмежується значеннями чисел Рейнольдса  (3.2)
(3.2) .
. залежить від числа Рейнольдса і діаметру трубопроводу і визначається по формулі
залежить від числа Рейнольдса і діаметру трубопроводу і визначається по формулі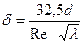 (3.3)
(3.3) . Діапазон гідравлічно гладких труб знаходиться при числах Рейнольдса 2300 <
. Діапазон гідравлічно гладких труб знаходиться при числах Рейнольдса 2300 < 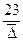 , де
, де  . Для визначення
. Для визначення  (3.4)
(3.4) (3.5)
(3.5)
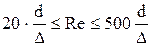
 ) виступів шорсткості
) виступів шорсткості  .
.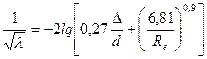 , (3.6)
, (3.6) , (3.7)
, (3.7) . (3.8)
. (3.8) (3.9)
(3.9) <<
<<  , або (3.10)
, або (3.10) (3.11)
(3.11)

 по п’єзометрам. Залежність між перепадом
по п’єзометрам. Залежність між перепадом  можна представити у виді співвідношення
можна представити у виді співвідношення ,
, – коефіцієнт витрати діафрагми, який визначають за допомогою тарування.
– коефіцієнт витрати діафрагми, який визначають за допомогою тарування.
 ,
,  – покази п’єзометрів на початку і кінці досліджуваної ділянки труби.
– покази п’єзометрів на початку і кінці досліджуваної ділянки труби.
 ,
, 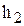 – рівень у мірному баку на початку і наприкінці замірів;
– рівень у мірному баку на початку і наприкінці замірів;
 – площа живого перерізу труби. (Діаметр d= 10 мм.)
– площа живого перерізу труби. (Діаметр d= 10 мм.)






 Δλ;
Δλ;

 – коефіцієнт кінематичної в'язкості, значення якого для виміряного значення температури приймається з таблиці додатку 1.
– коефіцієнт кінематичної в'язкості, значення якого для виміряного значення температури приймається з таблиці додатку 1.
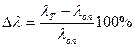
 .
.


