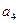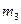Задача 4Вероятность того, что в результате проверки изделию будет присвоен знак «изделие высшего качества» равна p. 1) На контроль поступило n изделий. Какова вероятность того, что знак высшего качества будет присвоен: а) ровно m изделиям; б) более чем k изделиям; в) хотя бы одному изделию; г) указать наивероятнейшее количество изделий, получивших 2) При тех же условиях найти вероятность того, что в партии из N изделий знак высшего качества получает: а) ровно половина изделий; б) не менее чем 1. n = 6; p = 0,5; m = 4; k=5; N = 20; 2. n = 7; p = 0,6; m = 5; k=6; N = 26; 3. n = 8; p = 0,7; m = 4; k=3; N = 24; 4. n = 5; p = 0,4; m = 3; k=4; N = 30; 5. n = 6; p = 0,5; m = 2; k=7; N = 32; 6. n = 7; p = 0,6; m = 5; k=2; N = 28; 7. n = 8; p = 0,3; m = 6; k=3; N = 20; 8. n = 9; p = 0,2; m = 5; k=4; N = 22; 9. n = 6; p = 0,4; m = 3; k=2; N = 24; 10. n = 7; p = 0,6; m = 4; k=5; N = 20; 11. n = 8; p = 0,4; m = 5; k=6; N = 20; 12. n = 7; p = 0,3; m = 4; k=5; N = 24; 13. n = 6; p = 0,2; m = 3; k=4; N = 28; 14. n = 5; p = 0,3; m = 2; k=3; N = 30; 15. n = 4; p = 0,6; m = 1; k=2; N = 32; 16. n = 9; p = 0,2; m = 6; k=7; N = 34; 17. n = 7; p = 0,5; m = 3; k=4; N = 36; 18. n = 6; p = 0,4; m = 1; k=3; N = 38; 19. n = 8; p = 0,6; m = 4; k=5; N = 40; 20. n = 5; p = 0,5; m = 3; k=2; N = 26; Задача 5 В лотерее на каждые 100 билетов приходится Составить закон распределения величины выигрыша для владельца одного билета и найти его основные характеристики: математическое ожидание, дисперсию и среднее квадратическое отклонение. Пояснить смысл указанных характеристик.
|
, но не более, чем 
изделий.
билетов с выигрышем 
тыс. рублей, 
билетов с выигрышем 
тыс. рублей, т3 билетов с выигрышем а3 тыс. рублей и т.д. Остальные билеты из сотни не выигрывают.
