Методика решения задачи размещения
Считаются заданными: площадь региона Из очевидных геометрических соображений следует, что капитальные затраты на магистральные каналы связи между ВЦ можно определить из следующего выражения:
где Величина Основываясь на аналогичных рассуждениях, можно прийти к выводу, что минимизация суммарной длины каналов связи между ВЦ и АП также достигается при равномерном размещении АП в зоне обслуживания ВЦ. Исходя из изложенного, определяют капитальные вложения на создание всех ВЦ
Здесь Для конкретных структур сети ЭВМ значения
Найдем частные производные от полных затрат W по переменным R н г с целью определения экстремальных значений этих величин для функции W и приравняем их нулю:
Решая совместно эти два уравнения как систему путем подстановки, получим искомое соотношение, которое является уравнением 11-й степени относительно R:
Выражения для коэффициентов Найдя корни алгебраического уравнения, для данных значений коэффициентов, найдем множество значений корней 1) среднее расстояние между АП и ВЦ:
2) оптимальное число узлов (ВЦ в данном случае) в сети:
3) среднее число АП, подсоединяемых в каждом узле,
где Для топологического проектирования из перечисленных параметров наиболее важным является оптимальное число узлов в сети. В тех случаях, когда стоимость является главным критерием, синтез топологической структуры может быть проведен по минимуму этого критерия. Допустим, что для некоторых значений исходных данных Предположим, что в результате вычислений При первоначальных предположениях, считалось, что связи между узлами образуют полносвязную структуру. Однако в ходе синтеза архитектуры такой сети можно теоретически рассмотреть и другие варианты топологических структур, оценить, насколько возможно дальнейшее уменьшение стоимости, если это требуется. В дальнейшем при рассмотрении вопроса синтеза топологии ИС будем ориентироваться на простую структуру типа дерева, полагая, что таким образом можно понизить стоимость проектируемой сети и сравнить ее с максимальной, соответствующей полносвязной структуре. Для решения задачи минимизации структуры воспользуемся моделью сети в виде взвешенного графа, у которого веса дуг характеризуют, например, протяженности каналов между соответствующими узлами ИС. Так как рассматривается сеть с относительно малым числом ребер, для нее удобным способом решения задачи минимизации структуры является алгоритм Краскала, который заключается в следующем [1].
Рисунок 3 - План размещения узлов в синтезируемой сети
Упорядочим ребра по весу, выбирая из множества ребер графа, при составлении списка, каждый раз ребро минимального веса, и далее по возрастанию как показано в табл. 1. Затем, пользуясь списком, строим минимальное покрывающее дерево, начиная с первого ребра и добавляя последующие по порядку. Если очередное выбранное ребро приводит к образованию цикла, то его отбрасываем. После выбора ребра
Таблица 1 – Список ребер с их весовыми значениями
|

 , количество абонентов в сети
, количество абонентов в сети  , капитальные затраты на установку одного ВЦ и АП
, капитальные затраты на установку одного ВЦ и АП  и
и  соответственно; стоимость 1 км магистрального канала связи между ВЦ W3 и стоимость 1 км канала связи между АП и ВЦ
соответственно; стоимость 1 км магистрального канала связи между ВЦ W3 и стоимость 1 км канала связи между АП и ВЦ  . Нужно определить координаты установки ВЦ и АП, их количество в регионе, а также конфигурацию системы обмена данными, чтобы обеспечить минимум затрат и возможность обработки объемов информации.
. Нужно определить координаты установки ВЦ и АП, их количество в регионе, а также конфигурацию системы обмена данными, чтобы обеспечить минимум затрат и возможность обработки объемов информации. (9)
(9) — индекс рассматриваемого ВЦ;
— индекс рассматриваемого ВЦ;  — индексы находящегося правее и
— индексы находящегося правее и  — находящегося ниже ВЦ (см. рис. 2);
— находящегося ниже ВЦ (см. рис. 2);  —проекция прямой, связывающей
—проекция прямой, связывающей  не зависит от значений
не зависит от значений  и
и  . В то же время согласно неравенству Коши вторая сумма в квадратных скобках формулы (9) минимизируется при
. В то же время согласно неравенству Коши вторая сумма в квадратных скобках формулы (9) минимизируется при  для любых
для любых  к АП
к АП  в обслуживаемом регионе. Опуская промежуточные алгебраические преобразования в формулах, полученных из геометрических построений, приведем основное соотношение для постановки задачи минимизации затрат на проектируемую сеть:
в обслуживаемом регионе. Опуская промежуточные алгебраические преобразования в формулах, полученных из геометрических построений, приведем основное соотношение для постановки задачи минимизации затрат на проектируемую сеть: .
. и
и  — размеры зоны, заданной в виде прямоугольника со сторонами
— размеры зоны, заданной в виде прямоугольника со сторонами  и
и  для любого варианта могут быть вычислены следующим образом:
для любого варианта могут быть вычислены следующим образом: , (11)
, (11) , (12)
, (12) . (13)
. (13) (14)
(14) (15)
(15) в общем виде необычайно громоздки, поэтому рассмотрим пример расчета со следующими данными:
в общем виде необычайно громоздки, поэтому рассмотрим пример расчета со следующими данными:  [км2];
[км2];  ;
;  [тыс. грн.];
[тыс. грн.];  [тыс. грн.];
[тыс. грн.];  [тыс. грн./км];
[тыс. грн./км];  [тыс. грн./км].
[тыс. грн./км]. . Из этого множества, естественно, исключаются элементы, определяющие мнимые и отрицательные значения, остальные проверяются на соответствие физическому смыслу задачи. Выбрав одно наиболее подходящее значение
. Из этого множества, естественно, исключаются элементы, определяющие мнимые и отрицательные значения, остальные проверяются на соответствие физическому смыслу задачи. Выбрав одно наиболее подходящее значение  км, находим далее соответствующие этому значению величины, определяющие оптимальное распределение затрат для синтезируемой сети:
км, находим далее соответствующие этому значению величины, определяющие оптимальное распределение затрат для синтезируемой сети: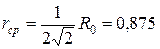 км;
км;

 — среднее число абонентов в одном узле.
— среднее число абонентов в одном узле. ,
,  ,
,  . Реальное размещение ВЦ по территории региона может не соответствовать равномерному их распределению. Но при небольшом числе узлов путем подбора конкретных мест расположения ВЦ можно выбрать наиболее близкий реальный вариант и принять его для последующего анализа.
. Реальное размещение ВЦ по территории региона может не соответствовать равномерному их распределению. Но при небольшом числе узлов путем подбора конкретных мест расположения ВЦ можно выбрать наиболее близкий реальный вариант и принять его для последующего анализа.
 (
( —число вершин графа) процесс заканчивается.
—число вершин графа) процесс заканчивается.


