Основные задачи оптимизации ИС
Рассмотрим некоторые типовые варианты оптимизационных задач, связанных с топологическим проектированием ИС. Возможна следующая их классификация [2]. 1. Выбор оптимальной пропускной способности (ВСП). Дано: топология сети, потоки, маршруты. Требуется: минимизировать задержки Т по переменной пропускной способности каналов
2. Распределение потока. Дано: топология сети, потоки, пропускные способности каналов. Требуется: минимизировать Т по переменной «маршрут движения» при заданных ограничениях на потоки. 3. Оптимальное распределение потоков и одновременно выбор пропускных способностей. Дано: топология сети, потоки. Требуется: минимизировать 4. Определение оптимальной топологии сети. Дано: характеристики трафика ИС. Требуется: минимизировать по переменным «топология», «маршрут» и «пропускная способность» при ограничениях на поток, задержки и топологию. Рассмотрим задачу оптимизации пропускных способностей линий. Высокая пропускная способность линий приводит к увеличению затрат, а при малой происходят перегрузки и задержки сообщений. Соотношение между стоимостью и пропускной способностью линий имеет вид
где W - полная стоимость линий; Wi - стоимостный коэффициент для i -линии; Ci- пропускная способность i -линии. Значения Wi неравные, потому что линии имеют разные длины. В частности, соотношение между стоимостью и пропускной способностью может быть задано степенным законом
Средняя задержка для
где Среднее значение задержки по всем составляющим получается путём усреднения значения
Искомые пропускные способности, которые минимизируют Т при постоянном W, определяются методом неопределенных множителей Лагранжа. Опуская соответствующие математические преобразования, приведем результат в готовом виде:
где
Первое слагаемое Величина результирующей транзитной задержки при передаче по линиям с пропускными способностями
где Рассмотренная задача позволяет при заданном ограничении на стоимость каналов связи так выбрать пропускные способности, чтобы средняя задержка сообщений была минимальной. К числу оптимизационных задач синтеза ИС относится задача распределения потоков. В предыдущей задаче выбирали пропускные способности каналов при заданной конфигурации потоков. В данной задаче пропускные способности заданы, а потоки надо распределить так, чтобы минимизировать среднюю задержку Т. Предполагается, что все пропускные способности удовлетворяют требованиям трафика, а процедуры выбора пути фиксированы и однозначны. В качестве исходного выражения для решения задачи используем приведенную выше формулу. В этом случае задача оптимального распределения потоков представляет собой минимизацию нелинейной функции Т по потокам Согласно этому закону суммарный трафик Доказывается, что при этих условиях и ограничениях Т есть выпуклая функция потоков, а множество реализуемых потоков представляется математической моделью в виде выпуклого многогранника в Часто при оптимизации ИС используется метод отклонения потока (ОП), суть которого заключается в нахождении стоимости сети для значений «длин»
такие «длины» или «стоимостные коэффициенты», соответствующие им, используют для формулировки задачи отыскания потоков по кратчайшим путям и выяснения вопроса о том, какая часть исходного потока должна быть отклонена. Процесс решения циклически повторяется до тех пор, пока не будут получены приемлемые значения
|

 при ограничениях на стоимость
при ограничениях на стоимость  и пропускные способности
и пропускные способности 
 ,
,
 й линии задается временем ожидания в очереди при допущениях, что длина сообщений имеет экспоненциальное распределение:
й линии задается временем ожидания в очереди при допущениях, что длина сообщений имеет экспоненциальное распределение: ,
, — интенсивность потока сообщений в
— интенсивность потока сообщений в  — средняя длина сообщений (в битах).
— средняя длина сообщений (в битах). взятого с весовыми коэффициентами
взятого с весовыми коэффициентами 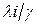 , где
, где  - суммарная скорость поступления сообщений. Таким образом, средняя задержка Т при этом определяется выражением
- суммарная скорость поступления сообщений. Таким образом, средняя задержка Т при этом определяется выражением (16)
(16)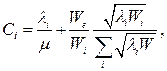 (17)
(17) — определяется выражением
— определяется выражением
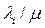 , в правой части формулы для
, в правой части формулы для  (18)
(18) - сумма интенсивностей трафика
- сумма интенсивностей трафика 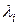 по всем линиям.
по всем линиям. при условиях выполнения закона сохранения потоков в каждом узле.
при условиях выполнения закона сохранения потоков в каждом узле. , поступающий в узел п, равен суммарному трафику
, поступающий в узел п, равен суммарному трафику  ; является узлом-источником или при
; является узлом-источником или при  - узлом назначения. На пропускные способности накладываются ограничения, состоящие в том, что поток
- узлом назначения. На пропускные способности накладываются ограничения, состоящие в том, что поток  в канале
в канале  не должен быть отрицательным и меньшим пропускной способности, т. е.
не должен быть отрицательным и меньшим пропускной способности, т. е.  .
. -мерном пространстве параметров потоков. Рассматриваемая задача решается симплекс-методом, который упоминался выше. Если она имеет реализуемое решение, то любой локальный минимум является глобальным минимумом для Т.
-мерном пространстве параметров потоков. Рассматриваемая задача решается симплекс-методом, который упоминался выше. Если она имеет реализуемое решение, то любой локальный минимум является глобальным минимумом для Т. (19)
(19) . Оптимальный алгоритм ОП дает минимальное значение Т - среднюю задержку сообщения в сети.
. Оптимальный алгоритм ОП дает минимальное значение Т - среднюю задержку сообщения в сети.


