Пользуясь правилом Лопиталя, найти пределы функций.
81. а) 83. а) 85. а) 87. а) 89. а) 91. а) 93. а) 95. а) 97. а) 99. а) Исследовать функцию и построить ее график. 101. 113. 117.
Решить системы по формулам Крамера и матричным способом.
121.
124.
127.
130.
133. 136.
139.
8. (141-160). Даны вершины треугольника А, В, С. Найти уравнение и длину высоты, опущенной из вершины В. Сделать чертеж. 141. 143. 145. 147. 149. 151. 153. 155. 157. 159. Литература 1. Апатенок Р.Ф., Маркина А.М. и др. Элементы линейной алгебры и аналитической геометрии. - Мн.: Выш. шк., 1986. 2. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. –М.: Наука, 1980, 1984, 1988. 3. Бугров Я.С., Никольский С.М. Дифференциальноеи интегральное исчисление. -М.: Наука, 1980, 1988. 4. Бугров Н.С., Никольский С.М. Высшая математика: Задачник. - М.: Наука, 1982. 5. Головина Л.И. Линейная алгебра и некоторые ее приложения. -М.: Наука, 1965. 6. Гусак А. А. Высшая математика: В 2 т. - Мн.: Изд-во БГУ, 1978, 1983. - Т. I, 2. 7. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: В 2 ч. - М.: Выс. шк., 1986. - Ч. I, 2. 8. Жевняк Р.М., Карпук А.А. Высшая математика: В 2 ч. - Мн.: Выс. шк., 1984, 1985. - Ч. I, 2. 9. Ильин В.А., Лозняк Э.Г. Аналитическая геометрия. - М.: Наука, 1981. 10. Ильин В.А., Позняк Э.Г. Линейная алгебра. - М.: Наука, 1983. 11. Ильин В.А., Нозняк Э.Г. Основы математического анализа. В 2ч. - М.: Наука, 1980, 1982. 12. Клетеник Д.В.. Сборник задач по аналитической геометрии. - М .; Наука, 1986. 13. Кудрявцев Л.Д. Краткий курс математического анализа. - М.: Наука, 1989. 14. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов: В 3 т. - М.: Наука, 1985 - Т. 1-3. 15. Сборник индивидуальных заданий по высшей математике: В 4-х ч./ Под ред. А.П.Рябушко. - Мн .: Выш. школа, 1990. - Ч.1-4. 16. Сухая Т.А., Бубнов В.Ф. Задачи по высшей математике: Учебное пособие: В 2 ч. - Мн.: Выш. школа, 1993.
|

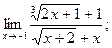 б)
б) 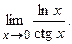 82. а)
82. а) 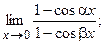 б)
б) 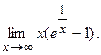
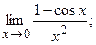 б)
б) 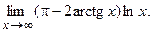 84. а)
84. а) 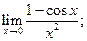 б)
б) 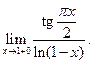
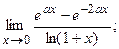 б)
б) 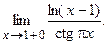 86. а)
86. а) 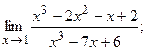 б)
б) 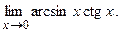
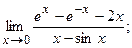 б)
б) 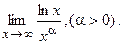 88. а)
88. а) 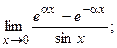 б)
б) 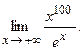
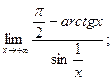 б)
б) 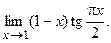 90. а)
90. а) 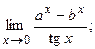 б)
б) 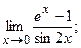 б)
б) 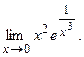 92. а)
92. а) 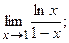 б)
б) 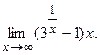
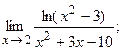 б)
б) 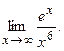 94. а)
94. а) 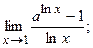 б)
б) 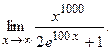
 б)
б)  96. а)
96. а) 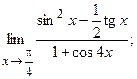 б)
б) 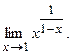
 б)
б) 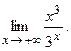 98. а)
98. а) 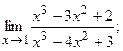 б)
б) 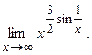
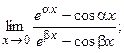 б)
б) 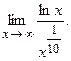 100. а)
100. а) 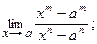 б)
б) 
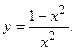 102.
102.  103.
103. 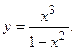 104.
104. 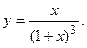 105.
105. 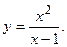 106.
106. 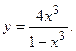 107.
107. 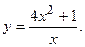 108.
108. 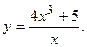 109.
109. 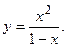 110.
110. 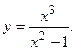 111.
111. 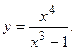 112.
112. 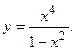
 114.
114. 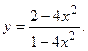 115.
115.  116.
116. 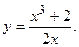
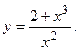 118.
118. 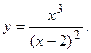 119.
119. 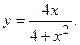 120.
120. 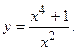
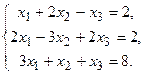 122.
122. 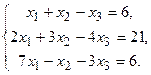 123.
123. 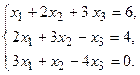
 125.
125. 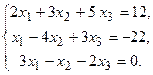 126.
126. 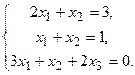
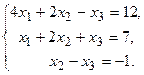 128.
128. 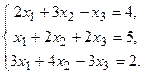 129.
129. 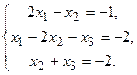
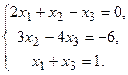 131.
131. 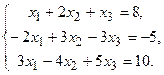 132.
132. 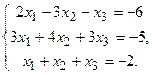
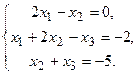 134.
134. 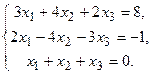 135.
135. 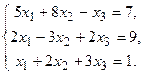
 137.
137. 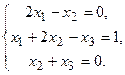 138.
138. 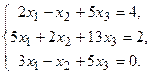
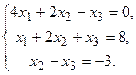 140.
140. 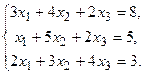
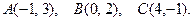 142.
142. 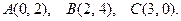
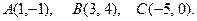 144.
144. 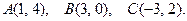
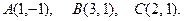 146.
146. 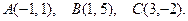
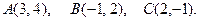 148.
148. 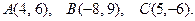
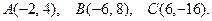 150.
150. 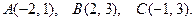
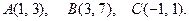 152.
152. 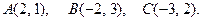 154.
154. 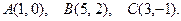
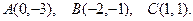 156.
156. 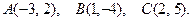
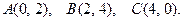 158.
158. 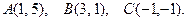
 160.
160. 


