Задание 16
Вычислить объём тела, ограниченного данными поверхностями. 1. 2. плоскости координат, плоскости x = 4, y = 4 и параболоид 3. цилиндрические поверхности 4. координатные плоскости, плоскость 2 x+ 3 y- 12 = 0 и цилиндр 5. цилиндр 6. цилиндр 7. 8. z = xy, цилиндр 9. 10.
Задание 17 Вычислить объём тела, ограниченного данными, переходя в тройном интеграле к цилиндрическим координатам. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
Задание 18 Переходя к сферическим координатам, вычислите интеграл:
1. 2.
3.
4.
5.
6.
7.
8.
9.
10. Вопросы к экзамену за 2 семестр [1]. Определение функции нескольких переменных. Предел функции нескольких переменных в точке. Двойной и повторные пределы. 2. Непрерывность функции нескольких переменных. Свойства непрерывных функций. 3. Частные производные функции нескольких переменных. Определение дифференцируемой функции в точке. Необходимые и достаточные условия дифференцируемости функции нескольких переменных. 4. Частные производные и дифференциалы высших порядков. [Формула Тейлора для функции нескольких переменных. Уравнение касательной плоскости к поверхности]. 5. Локальный экстремум функции нескольких переменных. Необходимые и достаточные условия локального экстремума. 6. Определение числового ряда. Сходящиеся и расходящиеся ряды. Необходимое условие сходимости ряда. 7. Критерий Коши сходимости числового ряда. 8. Свойства сходящихся рядов. 9. Ряды с неотрицательными членами. Критерий сходимости ряда с неотрицательными членами. Интегральный признак сходимости ряда. Признак сравнения. Следствия из признака сравнения. Признак Коши. Признак Даламбера. 10. Абсолютно и условно сходящиеся ряды. Знакочередующиеся ряды. Признак Лейбница. 11. Степенные ряды. Радиус, интервал сходимости, область сходимости. Теоремы Абеля. Свойства степенных рядов. [12]. Ряд Тейлора. Остаточный член формулы Тейлора в форме Пеано и в форме Лагранжа. Ряд Маклорена. Разложение основных элементарных функций в ряд Маклорена. 13. Определение двойного интеграла. Переход от двойного интеграла по элементарной области к повторному интегралу. 14. Замена переменных в двойном интеграле. Переход к полярным координатам. 15. Определение тройного интеграла. Переход от тройного интеграла по элементарной области к повторному интегралу. 16. Замена переменных в тройном интеграле. Переход к цилиндрическим и сферическим координатам. 17. Приложения кратных интегралов в геометрии и механике. [18]. Определение криволинейного интеграла первого рода. Вычисление криволинейных интегралов первого рода. Свойства и приложения криволинейных интегралов I рода. [19]. Определение криволинейного интеграла второго рода. Вычисление криволинейных интегралов второго рода. Свойства и приложения криволинейных интегралов II рода. [20]. Условия независимости криволинейного интеграла II рода от пути интегрирования. [21]. Формула Грина. [22]. Определение поверхностного интеграла первого рода. Вычисление поверхностных интегралов первого рода. Свойства и приложения поверхностных интегралов I рода. [23]. Определение поверхностного интеграла второго рода. Вычисление поверхностных интегралов второго рода. Свойства и приложения поверхностных интегралов II рода. [24]. Формула Остроградского-Гаусса и формула Стокса. [25].Разложение функций в ряд Фурье.
(Вопросы в квадратных скобках – для самостоятельного изучения)
|

 .
. .
. ,
,  и плоскости z = 0, x+z = 6.
и плоскости z = 0, x+z = 6. .
. , координатные плоскости и плоскость 3 x +4 y =12
, координатные плоскости и плоскость 3 x +4 y =12  .
.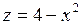 ,координатные плоскости и плоскость 2 x + y = 4
,координатные плоскости и плоскость 2 x + y = 4  .
. , z = 12- 3x- 4y, z = 1.
, z = 12- 3x- 4y, z = 1. .
.
 .
.

 .
. .
.
 .
. .
. .
. ,
, 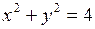 .
. .
. , где V – область, ограниченная поверхностью
, где V – область, ограниченная поверхностью  .
.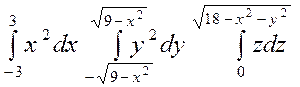 .
.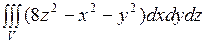 , где V – область, ограниченная сферой
, где V – область, ограниченная сферой  .
. , где V – область, ограниченная поверхностями:
, где V – область, ограниченная поверхностями:  ,
,  , y = 0, z = 0, y = x,
, y = 0, z = 0, y = x,  .
. , где V ограничена сферой
, где V ограничена сферой  и плоскостью z = 0
и плоскостью z = 0  .
. , где V – шар
, где V – шар  .
.
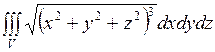 , где V - верхняя половина шара
, где V - верхняя половина шара  , где V ограничена сферой
, где V ограничена сферой  .
. , где V ограничена сферой
, где V ограничена сферой  и плоскостью х = 0
и плоскостью х = 0  .
. .
.


