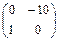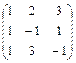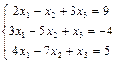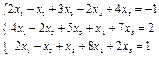Предлагаем Вам внимательно изучить нижеприведенную таблицу, где подробно показано, какие учебно-методические материалы студент получает от института, какой объем самостоятельной работы он должен выполнить в каждом семестре для получения итоговой оценки по курсу "Математика".
Распределение блока контроля в зависимости
От нормативного срока обучения
| Нормативный срок обучения
| Учебно-методическое обеспечение студента
| Семестр, в котором изучается курс
| Форма самостоятельной работы студента
|
| 3, 5 лет
| Методические указания
Учебно-методические материалы 1-4
|
| Три контрольные работы (№ 1, 2, 3, 4) + контрольные вопросы
|
| Методические указания
Учебно-методические материалы 5-7
|
| Три контрольные работы (№ 5, 6, 7) + контрольные вопросы
|
| Методические указания
Учебно-методические материалы 8
|
| Три контрольные работы (№ 8) + контрольные вопросы
|
| Методические указания
Учебно-методические материалы 9
|
| Три контрольные работы (№ 9) + контрольные вопросы
|
Контрольное задание №1
по разделу «Элементы линейной алгебры»
(задачи №№1–6, 10 вариантов)
Задача №1. Вычислить определитель четвертого порядка
| № варианта
| Определитель
| № варианта
| Определитель
|
|
| 
|
| 
|
|
| 
|
| 
|
|
| 
|
| 
|
|
| 
|
| 
|
|
| 
|
| 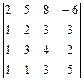
|
Задача №2. Даны матрицы А, В, С и числа a и b
а) Проверить, выполняются ли равенства:
1) (А+В)+С=А+(В+С) – сочетательный закон сложения матриц.
2) a×(b×С)=(a×b)×С – сочетательный закон умножения матрицы на число.

| распределительные законы.
| |
3) a×(А+В)=a×А+a×В
4) 
5) Найти матрицу, равную  .
.
| № варианта
| Матрица А
| Матрица В
| Матрица С
| Числа
|
| α
| b
|
|
| 
| 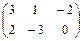
| 
| –2
|
|
|
| 
| 
| 
|
| –3
|
|
| 
| 
| 
|
| –2
|
|
| 
| 
| 
| –3
|
|
|
| 
| 
| 
|
| –2
|
|
| 
| 
| 
|
| –3
|
|
| 
| 
| 
|
| –3
|
|
| 
| 
| 
| –2
| –3
|
|
| 
| 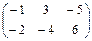
| 
| –2
|
|
|
| 
| 
| 
|
| –1
|
Задача №3. Проверить, выполняется ли равенство  .
.
| № варианта
| А
| В
| № варианта
| А
| В
|
|
| 
| 
|
| 
| 
|
|
| 
| 
|
| 
| 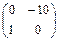
|
|
| 
| 
|
| 
| 
|
|
| 
| 
|
| 
| 
|
|
| 
| 
|
| 
| 
|
Задача № 4. Для данной матрицы найти обратную и убедиться, что обратная матрица найдена правильно
| № варианта
| Матрица
| № варианта
| Матрица
|
|
| 
|
| 
|
|
| 
|
| 
|
|
| 
|
| 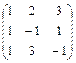
|
|
| 
|
| 
|
|
| 
|
| 
|
Задача №5. Доказать, что система крамеровская, и решить систему указанным способом. Правильность решения доказать
| № варианта
| Решить по формулам Крамера систему
| Решить матричным способом систему
|
|
| №1
| №5
|
|
| №2
| №7
|
|
| №3
| №8
|
|
| №4
| №10
|
|
| №5
| №9
|
|
| №6
| №1
|
|
| №7
| №2
|
|
| №8
| №3
|
|
| №9
| №4
|
|
| №10
| №6
|
№1 
| №6 
|
№2 
| №7 
|
№3 
| №8 
|
№4 
| №9 
|
№5 
| №10 
|
Задача № 6. Решить систему методом Гаусса
| № варианта
| Система
| № варианта
| Система
|
|
| 
|
| 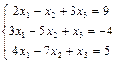
|
|
| 
|
| 
|
|
| 
|
| 
|
|
| 
|
| 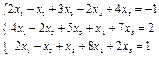
|
|
| 
|
| 
|










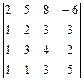


 .
.
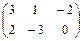























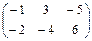




 .
.