Оптимизации САУ ЭП
Оптимизация основана на использовании желаемых передаточных функций, последовательной коррекции:
В связи с этим реальная передаточная функция системы определяется произведением величины неизменяемой части на передаточную функцию изменяемой части системы. Для того чтобы передаточная функция реальной системы равнялась желаемой, необходимо оперировать изменяемой частью, в качестве которой выступает регулятор с изменяемыми параметрами и структурой. Тогда для определения структуры и параметров регулятора, в соответствии с теорией последовательной коррекции, необходимо желаемую ПФ разделить на ПФ неизменяемой части:
Неизменяемая часть определяется передаточной функцией тиристорного преобразователя и двигателя. Структурная схема двухконтурной САУ ЭП (для регулируемого привода) представлена на рис. 8. В такой системе необходимо: - определить ПФ изменяемой части в первом контуре
- найти ПФ изменяемой части во втором контуре
Для решения задачи синтеза определяют выражения желаемых передаточных функций для первого и второго контура.
Рисунок 8 – Структурная схема регулируемого привода
Для этого используют следующие подходы: - технический оптимум (модульный принцип), который обеспечивает - симметричный оптимум, который обеспечивает погрешность, стремящуюся к нулю ( Принято, что желаемая передаточная функция
Отношение а =Ти/Та определяет вид переходного процесса, рис. 7. По выбранному желаемому переходному процессу оцениваются оптимальные параметры регулирования САУ ЭП.
1 — колебательный переходной процесс ( 2 — апериодический переходной процесс ( 3 — экспоненциальный переходной процесс (
Рисунок 7 – Виды переходного процесса в САУ ЭП
Для апериодического звена при допущении, что
Разновидности желаемых передаточных функций для различного вида переходных процессов представлены в табл.2. В таблице указаны оптимальные ПФ разомкнутых контуров регулирования в соответствии с желаемым переходным процессом в контуре.
Таблица 2 - Разновидности желаемых передаточных функций для различного вида переходных процессов
Примечание. Во внешних контурах или при переходе ко внешним контурам постоянные времени интегрирующего и апериодического звеньев увеличиваются в 2 раза с целью смещения ЛАЧХ внешних контуров в область низких частот (рис. 9). Если система оптимизируется по техническому оптимуму, то в системе до точки приложения нагрузки появляется одно интегрирующее звено, то есть искомый регулятор тока является ПИ-регулятором. Такие системы называются астатическими или системами с однократным интегрированием. Если необходимо увеличить точность регулирования, то применяют системы астатические второго порядка или с двукратным интегрированием. Тогда и в первом и во втором контурах образуются регуляторы типа ПИ. Таким образом, в системе начинают действовать два интегрирующих звена, выходной сигнал будет в противофазе со входным при сдвиге фаз 1800, и Для обеспечения устойчивости необходимо деформировать исходную ЛАЧХ путем ввода в систему форсирующего или дифференцирующего звена (создают сдвиг фаз — опережение). При этом ЛАЧХ желаемой передаточной функции этой системы примет симметричный вид по отношению к оси частот. Этот метод получил название симметричный оптимум.
Рисунок 9 – ЛАЧХ для двухконтурной системы
Таким образом, методика оптимизации будет следующей. 1 Составляется структурная схема двухконтурной САУ ЭП. 2 На схеме выделяются изменяемые и неизменяемые части. Изменяемая часть представлена регуляторами, структура которых может меняться. Неизменяемые части представлены реальными звеньями системы. 3 Выбирается вид желаемого оптимального переходного процесса: - для регулируемого привода — апериодический переходный процесс; - для следящего электропривода — монотонный (экспоненциальный переходный процесс). 4 Выбирают вид желаемой передаточной функции по виду переходного процесса и по виду привода. 5 Оптимизацию начинают с внутреннего контура в соответствии с принципом последовательной коррекции. 6 В результате преобразований получают передаточную функцию изменяемой части, в качестве которой выступают регуляторы: - во внутреннем контуре – регулятор тока (как правило ПИ регулятор); - во внешнем контуре – регулятор скорости (как правило, типа П – регулятора). Рассмотрим пример оптимизации двухконтурной системы АЭП.
Оптимизация внутреннего контура (
где Исходя из принципа последовательной коррекции, находим передаточную функцию регулятора тока (изменяемая часть):
Надо найти передаточную функцию для апериодического процесса (желаемую):
где Принимаем
где Пусть тогда
где
Таким образом, регулятор тока – это ПИ-регулятор, который расположен до точки приложения нагрузки. Первый контур реализован на астатической системе первого порядка (с однократным интегрированием).
Оптимизация внешнего контура (синтез регулятора скорости). Передаточную функцию замкнутого первого контура
Рисунок 10 – Структурная схема контура скорости
Синтез неизвестной неизменяемой части (регулятора скорости) производим в соответствии с методикой для контура тока (рис. 11).
где принимается, что
где
Рисунок 11 – Оптимизация контура скорости
Таким образом, в процессе синтеза контура скорости мы получили структуру П-регулятора.
|
.
,
.
:
;
:
.
.
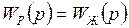, статическую погрешность 
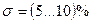и абсолютную устойчивость;
). Эти установки называются прецизионными.
состоит из двух идеальных звеньев: интегрирующего и апериодического:
.
; 
; 
)
; 
; 
)
; 
; 
)
.
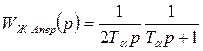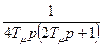
находятся в пределах от одной сотой до пяти тысячных - малая некомпенсируемая постоянная. Частота сопряжения 
.
система абсолютно неустойчива.
— частота среза; 
— частота сопряжения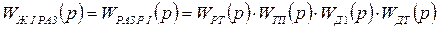
,
- неизвестная передаточная функция регулятора тока; 
- желаемая передаточная функция первого контура, разомкнутого; 
- передаточная функция, состоящая из реальных звеньев в разомкнутой системе; 
- передаточная функция датчика тока.
.
,
, 
... 
; 
.
или 
— одно и то же.
,
- ПИ-регулятор.
, а 
,
,
- пропорциональная часть (П),
- интегрирующая часть (И).
(рис. 10) находим по известным правилам для нахождения передаточных функций замкнутых систем.
,
.
,
,
.
,
; 
; 
; 
.
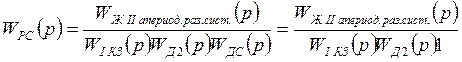