Сопряжения прямой с окружностью
Сопряжение прямой с окружностью может быть внешним или внутренним. Рассмотрим построение внешнего сопряжения прямой с окружностью. Пример 1. Пусть задана окружность радиусом R с центром в точке O1 и прямая m. Требуется построить сопряжение окружности с прямой дугой окружности заданного радиуса R (рис. 13). Для решения задачи выполним следующие построения. 1. Построим множество точек центров сопряжения, удаленных от сопрягаемой прямой на расстояние R. Это множество задает прямая m/, параллельная m и отстоящая от неё на расстояние R. 2. Множество точек центров сопряжения, удаленных от окружности n на расстояние R, есть окружность n /, проведенная радиусом R1 + R. 3. Центр сопряжения О находим как точку пересечения линий n / и m/. 4. Точку сопряжения А находим как основание перпендикуляра, проведенного из точки О на прямую m. Чтобы построить точку сопряжения В, необходимо провести линию центров OO1, т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В. 5.
Пример 2. При построении внутреннего сопряжения(рис. 14) последовательность построений остается та же, что и в примере 1. Однако центр сопряжения определяется с помощью вспомогательной дуги окружности, проведенной из центра О1, радиусом R - R1.
|
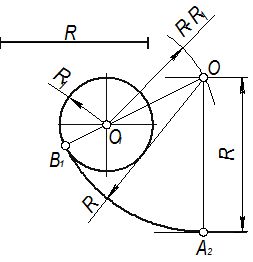
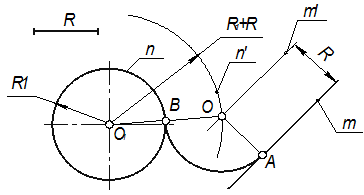Проведем дугу сопряжения АВ.
