Количественный анализ надежности автоматического загрузочного устройства к вертикальному хонинговальному станку Gehring KS 400-102
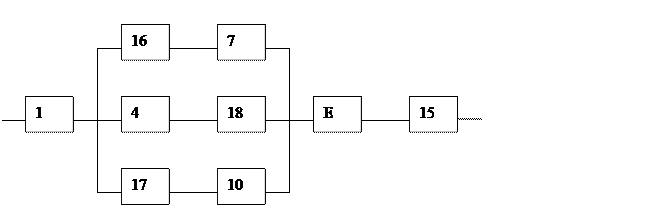
Автоматическое загрузочное устройство к вертикальному хонинговальному станку Gehring KS 400-102 состоит из 15 узлов, которые условно можно представить в виде схемы - рисунок 2.
Рисунок 2. Схема соединения основных узлов автоматического загрузочного устройства к вертикальному хонинговальному станку Gehring KS 400-102. Определим входные данные для расчета – интенсивность отказа каждого из узлов:
1. Преобразование системы разобьем на несколько этапов. Этап I представлен на рисунке 3.
Рисунок 3. Этап I преобразования схемы. 2. В исходной схеме элементы 2 и 3 образуют параллельное соединение. Заменяем их квазиэлементом 16.
3. Элементы 4 и 5 также образуют параллельное соединение, заменив которое элементом 17 и учитывая, что
4. Элементы 8 и 9 также образуют параллельное соединение, заменив которое элементом 18 и учитывая, что
5. Элементы 11, 12, 13 и 14 образуют соединение “2 из 4”, которое заменяем элементом Е. Так как, то для определения вероятности безотказной работы элемента E можно воспользоваться комбинаторным методом:
После первого этапа преобразования схема представлена на рисунке 4.
  

Рисунок 4. Этап II преобразования схемы. 6. Элементы 16 и 7 в исходной схеме соединены последовательно. Заменяем их элементом А, для которого
7. Элементы 4 и 18 в исходной схеме соединены последовательно. Заменяем их элементом В, для которого
8. Элементы 10 и 17 в исходной схеме соединены последовательно. Заменяем их элементом С, для которого:
9. Элементы A, B, C образуют параллельное соединение, следовательно заменяем их элементом D:
10. Таким образом, после преобразования схема выглядит следующим образом, смотри рисунок 5:
Рисунок 5. Преобразованная схема. В преобразованной схеме элементы 1, D, E и 15 образуют последовательное соединение. Тогда вероятность безотказной работы всей системы:
11. Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то вероятность безотказной работы элементов с 1 по 15 подчиняются экспоненциальному закону:
12. Результаты расчетов вероятностей безотказной работы элементов 1 - 15 исходной схемы по формуле (12) для наработки до Таблица 5
|


 (1)
(1)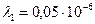 (2)
(2)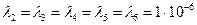

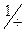
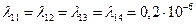
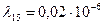
 (3)
(3)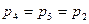 , получим:
, получим: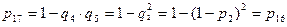 (4)
(4) , получим
, получим (5)
(5)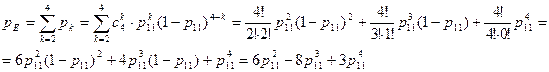 (6)
(6)
 (7)
(7)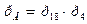 (8)
(8)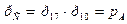 (9)
(9)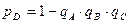 (10)
(10)







 (11)
(11) (12)
(12)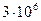 часов представлены в таблице 5.
часов представлены в таблице 5.


