Ребята, расстаются с Масленицей с большим сожалением: «Веселенько тебя встречать, привечать; трудно, нудно тебя со двора провожать!»
Масляная полизуха
Полизала сыр да масло,
А сама и погасла!
Масленица, прощай, н
На тот год опять приезжай!
Уходи, зима! Приходи, весна! Прощай, зима! Прощай, Масленица!
Звучит украинская народная песня «Веснянка».
Попытайтесь сочинить собственную песенку на народные масленичные стихи.
Спасибо за активную работу. Молодцы!
Матрица потребностей
| Признак потребности
| Характеристика признака
|
|
|
|
| 1. Место в иерархии
потребностей
| 1.1. Первичные (низшие)
1.1.1. Физиологические (голод, жажда, отсутствие
жилища, сексуальные потребности)
1.1.2. Безопасность, защищенность
1.2. Высшие
1.2.1. Социальные (принадлежность к социальной группе, потребность в уважении, признании)
1.2.2. Духовные
1.2.3. Потребность в самовыражении, самоактуализации, реализации творческих способностей
|
| 2. Что влияет на
потребность
| 2.1. Национальность
2.2. История
2.5. География
2.4. Природа
2.5. Пол
2.6. Возраст
2.7. Социальное положение
|
| 3. Историческое место
потребности
| 3.1. Прошлые
3.2. Настоящие
3.3. Будущие
|
| 4. Уровень
удовлетворения
потребности
| 4.1. Полностью удовлетворенные
4.2. Частично удовлетворенные
4.3. Неудовлетворенные
|
| 5. Степень
сопряженности
потребности
| 5.1 Слабо сопряженная с другими потребностями
5.2. Сопряженная
5.3. Сильно сопряженная (автолюбитель и бензин, лыжи и снег, электронные часы и батарейки и т.п.)
|
| 6. Масштаб
распространения
| 6.1. Географический: всеобщий, региональный
6.2. Социальный: всеобщий, внутри национальной общности, внутри социальной группы по образованию, внутри группы по доходу
|
| 7. Частота
удовлетворения
| 7.1. Единично удовлетворяемые
7.2. Периодически удовлетворяемые
7.3. Непрерывно удовлетворяемые
|
| 8. Природа
возникновения
| 8.1. Основные
8.2. Вторичные
8.3. Косвенные
|
| 9. Применяемость
потребности
| 9.1. В одной области
9.2. В нескольких областях
9.3. Во всех областях
|
| 10. Комплексность
удовлетворения
| 10.1. Удовлетворяется одним товаром
10.2. Удовлетворяется несколькими товарами
10.3. Удовлетворяется взаимозаменяемыми товарами
|
| 11. Отношение
общества
| 11.1. Отрицательное
11.2. Нейтральное
11.3. Положительное
|
| 12. Степень эластичности
от дохода и возраста
| 12.1. Слабоэластичные (для удовлетворения физиологических потребностей)
12.2. Эластичные (для удовлетворения высших потребностей)
12.3. Высокоэластичные (предметы роскоши)
|
| 13. Способ
удовлетворения
| 13.1. Индивидуальный
13.2. Групповой
13.3. Общественный
|
ЛАБОРАТОРНАЯ УСТАНОВКА
 Наиболее очевидный путь исследования прямолинейного движения тел под действием силы тяжести – это изучение свободного падения. Однако этому методу существенно препятствует большая величина ускорения при свободном падении. Действительно, при малой высоте прибора время падения тела составит малые доли секунды, и ошибки фиксации начала и конца движения окажутся соизмеримыми с временем падения. При большой же высоте прибора падающее тело наберет значительную скорость, и сила сопротивления воздуха окажется соизмеримой с силой тяжести, которая при малых скоростях движения возрастает пропорционально скорости тела. Это, в свою очередь, приведет к уменьшению ускорения. Преодолеть указанные трудности (уменьшив ускорение до приемлемых величин) позволяет устройство, получившее название «машина Атвуда».
Наиболее очевидный путь исследования прямолинейного движения тел под действием силы тяжести – это изучение свободного падения. Однако этому методу существенно препятствует большая величина ускорения при свободном падении. Действительно, при малой высоте прибора время падения тела составит малые доли секунды, и ошибки фиксации начала и конца движения окажутся соизмеримыми с временем падения. При большой же высоте прибора падающее тело наберет значительную скорость, и сила сопротивления воздуха окажется соизмеримой с силой тяжести, которая при малых скоростях движения возрастает пропорционально скорости тела. Это, в свою очередь, приведет к уменьшению ускорения. Преодолеть указанные трудности (уменьшив ускорение до приемлемых величин) позволяет устройство, получившее название «машина Атвуда».
Основой машины Атвуда (рис. 1) является вертикальная штанга 1 со шкалой. На верхнем торце штаги закреплен легкий блок 2, способный вращаться с незначительным трением. Через блок перекинута тонкая нить с прикрепленными грузами 3 одинаковых масс  . С помощью тормоза 4 грузы могут удерживаться в состоянии покоя. На штанге крепятся два кронштейна 5 и 6 с фотоэлектрическими датчиками. Фотоэлектрический датчик верхнего кронштейна формирует импульс напряжения, сигнализирующий о начале движения, датчик нижнего кронштейна – импульс, сигнализирующий о конце движения. Верхний кронштейн – подвижный, его можно перемещать вдоль штанги и фиксировать в любом положении, задавая таким образом длину пути груза. Нижний кронштейн – неподвижный, он оснащен платформой с резиновым амортизатором, в которую ударяется правый груз, завершая движение.
. С помощью тормоза 4 грузы могут удерживаться в состоянии покоя. На штанге крепятся два кронштейна 5 и 6 с фотоэлектрическими датчиками. Фотоэлектрический датчик верхнего кронштейна формирует импульс напряжения, сигнализирующий о начале движения, датчик нижнего кронштейна – импульс, сигнализирующий о конце движения. Верхний кронштейн – подвижный, его можно перемещать вдоль штанги и фиксировать в любом положении, задавая таким образом длину пути груза. Нижний кронштейн – неподвижный, он оснащен платформой с резиновым амортизатором, в которую ударяется правый груз, завершая движение.
 Если на правый груз положить перегрузок массой
Если на правый груз положить перегрузок массой  , то система грузов, связанных нитью, начнет двигаться с некоторым ускорением
, то система грузов, связанных нитью, начнет двигаться с некоторым ускорением  (рис. 2). Пренебрегая силой сопротивления воздуха, массой блока и силой трения в блоке, а также полагая нить нерастяжимой и невесомой, можно считать, что на каждый груз действуют две силы: сила тяжести груза и сила натяжения нити. Причем силы натяжения, действующие на оба груза, в этом случае одинаковы.
(рис. 2). Пренебрегая силой сопротивления воздуха, массой блока и силой трения в блоке, а также полагая нить нерастяжимой и невесомой, можно считать, что на каждый груз действуют две силы: сила тяжести груза и сила натяжения нити. Причем силы натяжения, действующие на оба груза, в этом случае одинаковы.
Направив ось  вертикально вниз и воспользовавшись вторым законом Ньютона, можно записать для каждого из грузов следующие уравнения движения:
вертикально вниз и воспользовавшись вторым законом Ньютона, можно записать для каждого из грузов следующие уравнения движения:
для правого груза
 , (1)
, (1)
для левого груза
 , (2)
, (2)
где  – ускорение свободного падения;
– ускорение свободного падения;
 – сила натяжения нити.
– сила натяжения нити.
Совместное решение уравнений (1) и (2) дает
 (3)
(3)
Из формулы (3) следует, что ускорение системы прямо пропорционально результирующей внешних сил, действующих на систему (в данном случае – силе тяжести перегрузка массой  ), и обратно пропорционально массе всей системы. В этом легко убедиться, записав второй закон Ньютона для всей системы «грузы – нить» в целом. При этом для наглядности систему целесообразно развернуть вдоль одной горизонтальной оси, выбрав ее направление, например, от одиночного груза к грузу с перегрузком (рис. 3):
), и обратно пропорционально массе всей системы. В этом легко убедиться, записав второй закон Ньютона для всей системы «грузы – нить» в целом. При этом для наглядности систему целесообразно развернуть вдоль одной горизонтальной оси, выбрав ее направление, например, от одиночного груза к грузу с перегрузком (рис. 3):

Рис. 3
Из рисунка видно, что результирующая внешних сил, приложенных к системе «грузы – нить», равна в соответствии со вторым законом Ньютона
 . (4)
. (4)
Формулы (3) и (4) справедливы лишь при условии принятых выше допущений. Здесь отметим, что масса блока и дополнительные внешние силы (сила трения в блоке и сила сопротивления воздуха) уменьшают величину ускорения.
Формулы кинематики для пути и скорости при прямолинейном равноускоренном движении имеют вид
 , (5)
, (5)
где  – начальная скорость тела;
– начальная скорость тела;
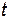 – время ускоренного движения.
– время ускоренного движения.
Используя формулы (5) и полагая в них  , ускорение тела можно найти по любой из двух формул:
, ускорение тела можно найти по любой из двух формул:
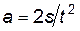 , (6)
, (6)
 . (7)
. (7)
Сопоставление значений ускорения, вычисленных по формулам (6) и (7), с величиной ускорения, рассчитанного по формуле (3), позволяет проверить кинематические формулы пути и скорости тела при равноускоренном движении, что и составляет содержание первых двух заданий работы.

 Наиболее очевидный путь исследования прямолинейного движения тел под действием силы тяжести – это изучение свободного падения. Однако этому методу существенно препятствует большая величина ускорения при свободном падении. Действительно, при малой высоте прибора время падения тела составит малые доли секунды, и ошибки фиксации начала и конца движения окажутся соизмеримыми с временем падения. При большой же высоте прибора падающее тело наберет значительную скорость, и сила сопротивления воздуха окажется соизмеримой с силой тяжести, которая при малых скоростях движения возрастает пропорционально скорости тела. Это, в свою очередь, приведет к уменьшению ускорения. Преодолеть указанные трудности (уменьшив ускорение до приемлемых величин) позволяет устройство, получившее название «машина Атвуда».
Наиболее очевидный путь исследования прямолинейного движения тел под действием силы тяжести – это изучение свободного падения. Однако этому методу существенно препятствует большая величина ускорения при свободном падении. Действительно, при малой высоте прибора время падения тела составит малые доли секунды, и ошибки фиксации начала и конца движения окажутся соизмеримыми с временем падения. При большой же высоте прибора падающее тело наберет значительную скорость, и сила сопротивления воздуха окажется соизмеримой с силой тяжести, которая при малых скоростях движения возрастает пропорционально скорости тела. Это, в свою очередь, приведет к уменьшению ускорения. Преодолеть указанные трудности (уменьшив ускорение до приемлемых величин) позволяет устройство, получившее название «машина Атвуда». . С помощью тормоза 4 грузы могут удерживаться в состоянии покоя. На штанге крепятся два кронштейна 5 и 6 с фотоэлектрическими датчиками. Фотоэлектрический датчик верхнего кронштейна формирует импульс напряжения, сигнализирующий о начале движения, датчик нижнего кронштейна – импульс, сигнализирующий о конце движения. Верхний кронштейн – подвижный, его можно перемещать вдоль штанги и фиксировать в любом положении, задавая таким образом длину пути груза. Нижний кронштейн – неподвижный, он оснащен платформой с резиновым амортизатором, в которую ударяется правый груз, завершая движение.
. С помощью тормоза 4 грузы могут удерживаться в состоянии покоя. На штанге крепятся два кронштейна 5 и 6 с фотоэлектрическими датчиками. Фотоэлектрический датчик верхнего кронштейна формирует импульс напряжения, сигнализирующий о начале движения, датчик нижнего кронштейна – импульс, сигнализирующий о конце движения. Верхний кронштейн – подвижный, его можно перемещать вдоль штанги и фиксировать в любом положении, задавая таким образом длину пути груза. Нижний кронштейн – неподвижный, он оснащен платформой с резиновым амортизатором, в которую ударяется правый груз, завершая движение. Если на правый груз положить перегрузок массой
Если на правый груз положить перегрузок массой  , то система грузов, связанных нитью, начнет двигаться с некоторым ускорением
, то система грузов, связанных нитью, начнет двигаться с некоторым ускорением  (рис. 2). Пренебрегая силой сопротивления воздуха, массой блока и силой трения в блоке, а также полагая нить нерастяжимой и невесомой, можно считать, что на каждый груз действуют две силы: сила тяжести груза и сила натяжения нити. Причем силы натяжения, действующие на оба груза, в этом случае одинаковы.
(рис. 2). Пренебрегая силой сопротивления воздуха, массой блока и силой трения в блоке, а также полагая нить нерастяжимой и невесомой, можно считать, что на каждый груз действуют две силы: сила тяжести груза и сила натяжения нити. Причем силы натяжения, действующие на оба груза, в этом случае одинаковы. вертикально вниз и воспользовавшись вторым законом Ньютона, можно записать для каждого из грузов следующие уравнения движения:
вертикально вниз и воспользовавшись вторым законом Ньютона, можно записать для каждого из грузов следующие уравнения движения: , (1)
, (1) , (2)
, (2) – ускорение свободного падения;
– ускорение свободного падения; – сила натяжения нити.
– сила натяжения нити. (3)
(3) ), и обратно пропорционально массе всей системы. В этом легко убедиться, записав второй закон Ньютона для всей системы «грузы – нить» в целом. При этом для наглядности систему целесообразно развернуть вдоль одной горизонтальной оси, выбрав ее направление, например, от одиночного груза к грузу с перегрузком (рис. 3):
), и обратно пропорционально массе всей системы. В этом легко убедиться, записав второй закон Ньютона для всей системы «грузы – нить» в целом. При этом для наглядности систему целесообразно развернуть вдоль одной горизонтальной оси, выбрав ее направление, например, от одиночного груза к грузу с перегрузком (рис. 3):
 . (4)
. (4) , (5)
, (5) – начальная скорость тела;
– начальная скорость тела;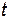 – время ускоренного движения.
– время ускоренного движения. , ускорение тела можно найти по любой из двух формул:
, ускорение тела можно найти по любой из двух формул: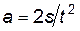 , (6)
, (6) . (7)
. (7)


