Билет 9. 1) Истинный и магнитный азимуты
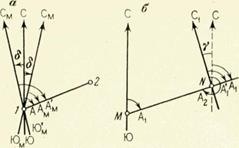
1) Истинный и магнитный азимуты. Склонение магнитной стрелки. Угол, отсчитываемый по ходу часовой стрелки от северного направления истинного меридиана до данного направления, называется истинным азимутом А (рис. 9, а). Истинный азимут изменяется от 0 до 360°. Угол, отсчитываемый по ходу часовой стрелки от северного направления магнитного меридиана до данного направления, называется магнитным азимутом Ам (см. рис. 9, а). Магнитный азимут, так же как и истинный, может изменяться от 0 до 360°. Магнитный меридиан, как правило, не совпадает с истинным в данной точке земной поверхности, образуя с ним некоторый угол б, называемый склонением магнитной стрелки.
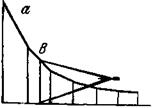
Угол б отсчитывается от истинного меридиана до магнитного и может быть восточным (со знаком плюс) и западным (со знаком минус). Зная склонение магнитной стрелки в данной точке, можно осуществить переход от магнитного азимута направления к истинному по формуле А = Ам + б, т. е. истинный азимут направления равен магнитному азимуту плюс склонение магнитной стрелки со своим знаком. 2) Определение крутизны скатов и уклонов линий по горизонталям. Графики заложений. Крутизна ската (угол наклона ската) V и уклон линий i между точками, лежащими на соседних горизонталях, определяются по известной формуле: I=tgv=h/d. V=arctgh/d. H – высота рельефа. d – заложение. Чтобы избежать расчетов при определении уклонов и крутизны скатов по плану или карте, на практике пользуются специальными графиками, называемыми графиками заложений. Для построения графика заложений горизонтальную линию делят на равные отрезки произвольной длины и у концов отрезков подписывают значения углов наклона, начиная с 30'. Предельное значение углов на шкале графика назначают в зависимости от максимальной крутизны скатов данного плана или карты. Затем вычисляют заложения, соответствующие каждому значению угла наклона при принятой высоте сечения рельефа, по формуле D=h/tgv. Полученные величины заложений, выраженные в масштабе плана (карты), откладывают на перпендикулярах к горизонтальной линии против соответствующих углов наклона. Через полученные точки проводят плавную линию и получают график заложений, называемый в данном случае графиком крутизны.
|

 (4)
(4)


