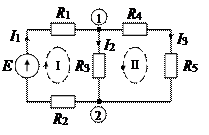
Часть 1 – Расчет по законам Кирхгофа.
1) определяем топологию цепи общее количество ветвей р * = 3 количество ветвей с источниками тока р ит = 0 количество ветвей с неизвестными токами р = (р *– р ит) = 3 – 0 = 3 количество узлов q = 2 количество независимых контуров n = p – (q – 1) = 3 – (2 – 1) = 2 2) составляем (q – 1) узловых уравнений по первому закону Кирхгофа узел 2: – I 1 + I 2 + I 3 = 0 3) составляем n контурных уравнений по второму закону Кирхгофа контур I: (R 1 + R 2)· I 1 + R 3· I 2 = Е контур II: R 3· I 2 – (R 4 + R 5)· I 3 = 0 4) объединяем узловые и контурные уравнения в системе
5) представляем полученную систему уравнений в матричной форме A·X=F
6) решение системы уравнений ищем в виде X = A- 1× F
Часть 2 – Расчет методом контурных токов
1) определяем собственные и общие сопротивления R 11 = R 1 + R 2 + R 3 = 5 + 15 + 40 = 60 Ом R 22 = R 3 + R 4 + R 5 = 40 + 35 + 85 = 160 Ом R 12 = R 12 = – R 3 = – 40 Ом 2) определяем контурные ЭДС Е 11 = Е = 100 В Е 22 = 0 В 3) составляем систему уравнений
и представляем ее в матричной форме 4) ищем решение системы уравнений
5) определяем неизвестные токи I 1 = I 11 = 2 А I 2 = I 11 – I 22 = 2 – 0.5 = 1.5 А I 3 = I 22 = 0.5 А Часть 3 – Расчет методом узловых напряжений
1) определяем собственные и общие проводимости g 11 = 2) определяем токи, обусловленные источниками энергии в цепи J 11 = E /(R 1 + R 2) = 100/(5+15) = 5 А 3) составляем систему уравнений g 11· U 10 = J 11, подставив численные значения получаем U 10/12 = 5 4) ищем решение системы уравнений U 10 = 60 В 5) определяем искомые токи I 1 = (E – U 10)/(R 1+ R 2) = (100 – 60)/(5+20) = 2 А I 2 = U 10/ R 3 = 60/40 = 1.5 А I 3 = U 10/(R 4+ R 5) = 60)/(35+85) = 0.5 А
|


 , подставив численные значения, получаем
, подставив численные значения, получаем
 А.
А.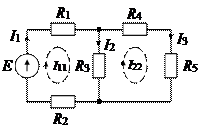
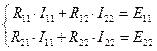
 , подставив численные значения, получаем
, подставив численные значения, получаем  .
. А.
А.
 См
См


