Основні наслідки мультиколінеарності.
1. Падає точність оцінювання, яка виявляється так: а) помилки деяких конкретних оцінок стають занадто великими; б) ці помилки досить корельовані одна з одною; в) дисперсії оцінок параметрів різко збільшуються. 2. Оцінки параметрів деяких змінних моделі можуть бути незначущими через наявність їх взаємозв'язку з іншими змінними, а не тому, що вони не впливають на залежну змінну. У такому разі множина вибіркових даних не дає змоги цей вплив виявити. 3. Оцінки параметрів стають досить чутливими до обсягів сукупності спостережень. Збільшення сукупності спостережень іноді може спричинитися до істотних змін в оцінках параметрів. З огляду на перелічені наслідки мультиколінеарності при побудові економетричної моделі потрібно мати інформацію про те, що між пояснювальними змінними не існує мультиколінеарністі. Ознаки мультиколінеарності такі. 1. Коли серед парних коефіцієнтів кореляції пояснювальних змінних є такі, рівень яких наближається або дорівнює множинному коефіцієнту кореляції, то це означає можливість існування мультиколінеарності. Інформацію про парну залежність може дати симетрична матриця коефіцієнтів парної кореляції або кореляції нульового порядку між пояснювальними змінними:
Проте, коли до моделі входять більш як дві пояснювальні змінні, то вивчення питання про мультиколінеарність не може обмежуватись інформацією, що її дає ця матриця. Явище мультиколінеарності в жодному разі не зводиться лише до існування парної кореляції між незалежними змінними. Більш загальна перевірка передбачає знаходження визначника (детермінанта) матриці r, який називається детермінантом кореляції і позначається | r |. Числові значення детермінанта кореляції задовольняють умову: | r | 2. Якщо | r | = 0, то існує повна мультиколінеарність, а коли | r | = 1, мультиколінеарність відсутня. Чим ближче | r | до нуля, тим певніше можна стверджувати, що між пояснювальними змінними існує мультиколінеарність. Незважаючи на те, що на числове значення | r | впливає дисперсія пояснювальних змінних, цей показник можна вважати точковою мірою рівня мультиколінеарності. 3. Якщо в економетричній моделі знайдено мале значення параметра âk при високому рівні частинного коефіцієнта детермінації 4. Коли коефіцієнт частинної детермінації 5. Нехай при побудові економетричної моделі на основі покрокової регресії введення нової пояснювальної змінної істотно змінює оцінку Усі ці ознаки мультиколінеарності мають один спільний недолік: ні одна з них чітко не розмежовує випадки, коли мультиколінеарність істотна і коли нею можна знехтувати. Найповніше дослідити мультиколінеарність можна за допомогою алгоритму Фаррара–Глобера. Цей алгоритм має три види статистичних критеріїв, згідно з якими перевіряється мультиколінеарність усього масиву незалежних змінних (χ2 – «хі»-квадрат); кожної незалежної змінної з рештою змінних (F -критерій); кожної пари незалежних змінних (t-критерій). Усі ці критерії при порівнянні з їх критичними значеннями дають змогу робити конкретні висновки щодо наявності чи відсутності мультиколінеарності незалежних змінних.
Опишемо алгоритм Фаррара–Глобера. Крок 1. Стандартизація (нормалізація) змінних. Позначимо вектори незалежних змінних економетричної моделі через х1, х2, х3... хm. Елементи стандартизованих векторів обчислимо за формулами:
де n – число спостережень (і =
Крок 2. Знаходження кореляційної матриці, виходячи з двох методів нормалізації змінних
де X* – матриця стандартизованих незалежних (пояснювальних) змінних;
Крок 3. Визначення критерію χ2 («хі»-квадрат):
де | r | – визначник кореляційної матриці r. Значення цього критерію порівнюється з табличним при
Крок 4. Визначення оберненої матриці:
Крок 5. Обчислення F -критеріїв:
де ckk – діагональні елементи матриці С. Фактичні значення критеріїв порівнюються з табличними при n-m і m- 1 ступенях вільності і рівні значущості α. Якщо Fk факт > F табл., то відповідна k -та незалежна змінна мультиколінеарна з іншими. Коефіцієнт детермінації для кожної змінної
Крок 6. Знаходження частинних коефіцієнтів кореляції:
де ckj – елемент матриці С, що міститься в k -му рядку і j -му стовпці; ckk і cjj – діагональні елементи матриці С.
Крок 7. Обчислення t - критеріїв:
Фактичні значення критеріїв tkj порівнюються з табличними при n-m ступенях вільності і рівні значущості α. Якщо tkj( ф) >t табл., то між незалежними змінними xk і xj існує мультиколінеарність.
Розглянемо застосування алгоритму Фаррара–Глобера для розв'язування конкретної задачі.
Приклад. На середньомісячну заробітну плату впливає ряд чинників. Вирізнимо серед них продуктивність праці, фондомісткість та коефіцієнт плинності робочої сили. Щоб побудувати економетричну модель заробітної плати від згаданих чинників згідно з методом найменших квадратів, потрібно переконатися, що продуктивність праці, фондомісткість та коефіцієнт плинності робочої сили як незалежні змінні моделі – не мультиколінеарні. Вихідні дані наведені в табл. 1. Таблиця 1
Дослідити наведені чинники на наявність мультиколінеарності.
|

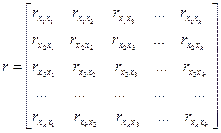
 [0,1].
[0,1]. і при цьому F -критерій істотно відрізняється від нуля, то це також свідчить про наявність мультиколінеарності.
і при цьому F -критерій істотно відрізняється від нуля, то це також свідчить про наявність мультиколінеарності.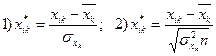 ,
,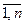 ); m – число пояснювальних змінних (k =
); m – число пояснювальних змінних (k = 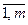 );
); 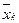 – середнє арифметичне k-ї пояснювальної змінної;
– середнє арифметичне k-ї пояснювальної змінної;  – дисперсія k -ї пояснювальної змінної.
– дисперсія k -ї пояснювальної змінної. ,
, – матриця, транспонована до матриці X*.
– матриця, транспонована до матриці X*.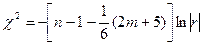 ,
, ступенях вільності і рівні значущості α. Якщо χ2факт >χ2табл, то в масиві пояснювальних змінних існує мультиколінеарність.
ступенях вільності і рівні значущості α. Якщо χ2факт >χ2табл, то в масиві пояснювальних змінних існує мультиколінеарність.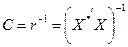 .
. ,
, .
.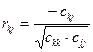 ,
,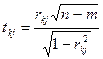 .
.


