Розв 'язания
Крок 1. Нормалізація змінних.
Позначимо вектори незалежних змінних – продуктивності праці, фондомісткості, коефіцієнтів плинності робочої сили – через x1, x2, x3. Елементи стандартизованих векторів обчислимо за формулою:
 , ,
де n – кількість спостережень, n =10; m – число незалежних змінних, m =3; 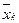 – середнє арифметичне значення вектора xk; – середнє арифметичне значення вектора xk;  – дисперсія змінної xk. – дисперсія змінної xk.
Із формули бачимо, що спочатку потрібно обчислити середні арифметичні для кожної пояснювальної змінної:
 ; ; 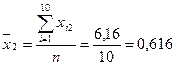 ; ;
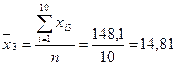 . .
Усі розрахункові дані для стандартизації змінних x1, x2, x3 згідно з поданими співвідношеннями наведено в табл. 2.
2.Розрахунок нормалізованих змінних
| №
| 
| 
| 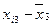
| 
| 
| 
| 
| 
| 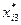
| |
| 3,3
0,3
1,3
2,3
-3,7
5,3
0,3
-4,7
-8,7
4,3
| 0,274
-0,186
0,084
-0,006
-0,106
-0,106
0,034
-0,186
-0,106
0,304
| 4,69
0,79
-1,31
-5,31
8,69
-2,31
2,69
-0,31
-0,31
-7,31
| 10,89
0,09
1,69
5,29
13,69
28,09
0,09
22,09
75,69
18,49
| 0,075076
0,034596
0,007056
0,000036
0,011236
0,011236
0,001156
0,034596
0,011236
0,092416
| 11,56
2,56
0,16
19,36
92,16
1,96
12,96
0,36
0,36
40,96
| 0,2487
0,0226
0,0980
0,1733
-0,2788
0,3994
0,0226
-0,3541
-0,6556
0,3240
| 0,0091
-0,3531
0,2580
0,0543
-0,1720
-0,1720
0,1448
-0,3531
-0,1720
0,7559
| -0,2518
0,1185
-0,0296
-0,3258
0,7108
-0,1037
0,2666
0,0444
0,0444
-0,4739
| |
Σ
|
|
|
| 176,1
| 0,278640
| 182,4
|
|
|
|
Дисперсії кожної незалежної змінної мають такі значення:
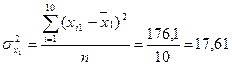 ; ;  ; ;
 . .
Тоді знаменник для стандартизації кожної незалежної змінної буде такий:
 ; ;
 ; ;
 . .
Матриця стандартизованих змінних подається у вигляді:

Крок 2. Знаходження кореляційної матриці:
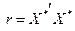 , ,
де X* – матриця нормалізованих пояснювальних змінних;  – матриця, транспонована до матриці X*. – матриця, транспонована до матриці X*.
Ця матриця симетрична і має розмір 3x3.
Для даної задачі

Кожний елемент цієї матриці характеризує тісноту зв'язку однієї незалежної змінної з іншою. Оскільки діагональні елементи характеризують тісноту зв'язку кожної незалежної з цією самою змінною, то вони дорівнюють одиниці. Зауважимо, що при знаходженні добутку матриць  і X* за рахунок зміщеності коефіцієнтів парної кореляції числові значення діагональних елементів можуть наближатись до одиниці. Якщо це так, то вони заміняються одиницями, а інші значення матриці r збільшуються на величину, що визначається як різниця між одиницею і діагональним елементом. і X* за рахунок зміщеності коефіцієнтів парної кореляції числові значення діагональних елементів можуть наближатись до одиниці. Якщо це так, то вони заміняються одиницями, а інші значення матриці r збільшуються на величину, що визначається як різниця між одиницею і діагональним елементом.
Інші елементи матриці r дорівнюють:
 ; ;
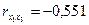 ; ;
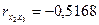 , ,
тобто вони є парними коефіцієнтами кореляції між пояснювальними змінними. Користуючись цими коефіцієнтами, можна зробити висновок, що між змінними x1, x2, x3 існує зв'язок. Але чи можна стверджувати, що цей зв'язок є виявленням мультиколінеарності, а через це негативно впливатиме на оцінку економетричної моделі?
Щоб відповісти на це запитання, потрібно ще раз звернутися до алгоритму Фаррара–Глобера і знайти статистичні критерії оцінки мультиколінеарності.
Крок 3. Обчислимо детермінант кореляційної матриці r і критерій χ;2:
а)  ; ;
б)  . .
При ступені вільності  =3 і рівні значущості α=0,01 критерій χ2табл.=11,34. Оскільки χ2факт <χ2табл., робимо висновок, що в масиві пояснювальних змінних не існує мультиколінеарності. =3 і рівні значущості α=0,01 критерій χ2табл.=11,34. Оскільки χ2факт <χ2табл., робимо висновок, що в масиві пояснювальних змінних не існує мультиколінеарності.
Крок 4. Знайдемо матрицю, обернену до матриці r:
 ; ;
 . .
Крок 5. Використовуючи діагональні елементи матриці С, обчислимо F -критерії:
 ; ;
 ; ;
 . .
Для рівня значущості α = 0,05 і ступенів вільності γ1 = 7 і γ2 = 2 критичне (табличне) значення критерію F = 4,74.
Оскільки
F 1факт< F табл;
F 2факт< F табл;
F 3факт< F табл,
то кожна з пояснювальних змінних не мультиколінеарна з двома іншими.
Щоб визначити наявність попарної мультиколінеарності, продовжимо дослідження і перейдемо до кроку 6.
Крок 6. Обчислимо частинні коефіцієнти кореляції, скориставшись елементами матриці С:
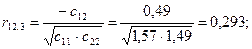
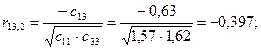
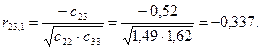
Частинні коефіцієнти кореляції характеризують тісноту зв'язку між двома змінними за умови, що третя не впливає на цей зв'язок.
Порівнявши частинні коефіцієнти кореляції з парними, які було наведено раніше, можна помітити, що частинні коефіцієнти значно менші за парні. Це ще раз показує, що на підставі парних коефіцієнтів кореляції не можна зробити висновків про наявність мультиколінеарності чи її відсутність.
Крок 7. Визначимо t -критерій на основі частинних коефіцієнтів кореляції.
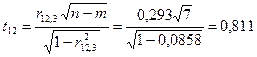 ; ;
 ; ;
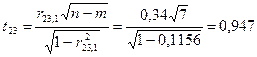 . .
Табличне значення t -критерію при n-m = 7 ступенях вільності і рівні значущості α = 0,05 дорівнює 1,69. Усі числові значення t -критеріїв, знайдених для кожної пари змінних, менші за їх табличні значення. Звідси робимо висновок, що всі пари незалежних змінних не є мультиколінеарними.
Отже, усі пояснювальні змінні досліджуваної моделі не мультиколінеарні.
Якщо F -критерій більший за табличне значення, тобто коли k-та змінна залежить від усіх інших у масиві, то необхідно вирішувати питання про її вилучення з переліку змінних.
Якщо tkj – критерій більший за табличний, то ці дві змінні (k і j) тісно пов'язані одна з одною. Звідси, аналізуючи рівень обох видів критеріїв F і t, можна зробити обгрунтований висновок про те, яку зі змінних необхідно вилучити з дослідження або замінити іншою. Проте заміна масиву незалежних змінних завжди має узгоджуватись з економічною доцільністю, що випливає з мети дослідження.
Найпростіше позбутися мультиколінеарності в економетричній моделі можна, відкинувши одну зі змінних мультиколінеарної пари. Але на практиці вилучення якогось чинника часто суперечить логіці економічних зв'язків. Тоді можна перетворити певним чином пояснювальні змінні моделі:
а) узяти відхилення від середньої;
б) замість абсолютних значень узяти відносні;
в) стандартизувати пояснювальні змінні тощо.
За наявності мультиколінеарності змінних потрібно звертати увагу й на специфікацію моделі. Іноді заміна однієї функції іншою, якщо це не суперечить апріорній інформації, дає змогу уникнути явища мультиколінеарності.
Коли жодний з розглянутих способів не дає змоги позбутися мультиколінеарності, то параметри моделі слід оцінювати за методом головних компонентів.
Контрольні запитання
1. Що означає мультиколінеарність змінних?
2. ознаки мультиколінеарності.
3. Як впливає наявність мультиколінеарність змінних на оцінку параметрів моделі?
4. Які статистичні критерії використовуються для виявлення мультиколінеарності?
5. Дайте коротку характеристику алгоритму Фаррара–Глобера.
Завдання для самостійної роботи
Завдання №1. Побудувати множинну економетричну модель за даними табл. 1-8 методом найменших квадратів та перевірити наявність мультиколінеарності за алгоритмом Фаррара-Глобера.
Табл. 1 Табл. 2
| №
| Y
| X1
| X2
| X3
|
| №
| Y
| X1
| X2
| X3
| |
| 55,26
| 7,5
| 11,8
| 9,7
|
| 54,26
| 8,5
| 11,8
| 9,8
| |
| 47,34
| 9,4
| 10,8
| 9,4
|
| 49,34
| 9,4
| 10,5
| 7,4
| |
| 52,34
| 11,4
| 11,9
| 9,1
|
| 52,34
| 11,4
| 11,9
| 9,1
| |
| 72,48
| 15,4
| 12,8
| 7,9
|
| 73,48
| 11,4
| 13,8
| 7,9
| |
| 67,34
| 12,3
| 12,4
| 8,4
|
| 67,34
| 12,3
| 12,4
| 8,4
| |
| 46,37
| 6,8
| 13,1
| 10,1
|
| 46,37
| 6,8
| 13,1
| 10,1
| |
| 61,37
| 7,9
| 15,4
| 9,7
|
|
| 64,37
| 7,9
| 17,4
| 9,7
| |
| 86,14
| 10,4
| 13,9
| 10,6
|
| 86,14
| 10,4
| 13,9
| 10,6
| |
| 91,34
| 11,6
| 14,5
| 11,4
|
| 91,34
| 11,6
| 14,5
| 12,4
| |
| 97,34
| 9,8
| 14,7
| 10,1
|
| 97,34
| 9,8
| 14,7
| 10,1
| |
| 101,54
| 11,4
| 15,1
| 11,7
|
| 107,54
| 21,4
| 15,1
| 11,7
| |
| 137,89
| 10,6
| 11,4
| 9,9
|
| 110,89
| 10,6
| 11.4
| 9,9
| |
| 124,69
| 11,8
| 15,9
| 10,8
|
| 124,69
| 11,8
| 15,9
| 18,8
| |
| 119,34
| 12,7
| 16,2
| 11,5
|
| 119,34
| 12,7
| 16,2
| 11,5
| |
| 134,27
| 13,7
| 16,8
| 11,5
|
| 142,27
| 13,7
| 16,8
| 11,5
| |
| 148,94
| 14,3
| 17,5
| 12,4
|
|
| 148,94
| 14,3
| 16,5
| 12,4
| |
| 147,37
| 14,9
| 18,9
| 12,9
|
| 147,37
| 15,9
| 17,9
| 15,9
| |
| 155,74
| 16,5
| 18,4
| 13,7
|
| 150,74
| 15,5
| 18,8
| 14,7
| Табл. 3 Табл. 4
| №
| Y
| X1
| X2
| X3
|
| №
| Y
| X1
| X2
| X3
| |
| 62,37
| 8,1
| 12,8
| 10,7
|
| 55,06
| 8,8
| 11,8
| 9,7
| |
| 49,34
| 9,4
| 10,5
| 8,4
|
| 49,34
| 10,1
| 10,5
| 8,4
| |
| 52,34
| 11,4
| 11,9
| 9,1
|
| 52,34
| 12,1
| 11,9
| 9,1
| |
| 73,48
| 15,4
| 12,8
| 7,9
|
| 73,48
| 16,1
| 12,8
| 8,4
| |
| 67,34
| 12,3
| 12,4
| 8,4
|
| 67,34
| 13,0
| 12,4
| 8,4
| |
| 48,64
| 7,2
| 14,2
| 11,7
|
| 54,7
| 7,9
| 12,7
| 10,7
| |
| 64,37
| 7,9
| 14,4
| 9,7
|
|
| 67,34
| 8,6
| 14,4
| 9,7
| |
| 86,14
| 10,4
| 13,9
| 10,6
|
| 86,14
| 11,1
| 13,9
| 10,6
| |
| 91,34
| 11,6
| 14,5
| 11,4
|
| 91,34
| 12,3
| 14,5
| 11,4
| |
| 97,34
| 9,8
| 14,7
| 10,1
|
| 97,34
| 10,5
| 14,7
| 10,1
| |
| 101,54
| 11,4
| 15,1
| 11,7
|
| 89,54
| 12,1
| 14,8
| 11,7
| |
| 125,27
| 11,8
| 20,4
| 10,7
|
| 99,40
| 12,5
| 9,4
| 8,7
| |
| 124,69
| 11,8
| 15,9
| 10,8
|
| 124,69
| 12,5
| 15,9
| 10,8
| |
| 119,34
| 12,7
| 16,2
| 11,5
|
| 119,34
| 13,4
| 16,2
| 12,5
| |
| 134,27
| 13,7
| 16,8
| 9,4
|
| 137,27
| 14,4
| 16,8
| 11,5
| |
| 148,37
| 14,3
| 17,5
| 12,4
|
|
| 148,94
| 15,0
| 17,5
| 12,4
| |
| 147,37
| 14,9
| 17,9
| 12,9
|
| 147,37
| 15,6
| 17,9
| 12,9
| |
| 150,74
| 15,5
| 18,4
| 13,7
|
| 147,20
| 16,2
| 19,4
| 15,5
| Табл. 5 Табл. 6
| №
| Y
| X1
| X2
| X3
|
| №
| Y
| X1
| X2
| X3
| |
| 62,37
| 8,1
| 12,8
| 10,7
|
| 67,71
| 10,4
| 16,7
| 13,2
| |
| 49,34
| 9,4
| 10,5
| 8,4
|
| 54,68
| 10,1
| 10,5
| 10,9
| |
| 52,34
| 11,4
| 11,9
| 9,1
|
| 57,68
| 12,1
| 11,9
| 11,6
| |
| 73,48
| 15,4
| 12,8
| 7,9
|
| 78,82
| 16,1
| 12,8
| 10,4
| |
| 67,34
| 12,3
| 12,4
| 8,4
|
| 72,68
| 13,0
| 12,4
| 10,9
| |
| 54,37
| 7,2
| 14,2
| 11,7
|
| 59,71
| 7,9
| 12,7
| 14,2
| |
| 64,37
| 7,9
| 14,4
| 9,7
|
|
| 69,71
| 8,6
| 14,4
| 12,2
| |
| 86,14
| 10,4
| 13,9
| 10,6
|
| 91,48
| 11,1
| 13,9
| 13,1
| |
| 91,34
| 11,6
| 14,5
| 11,4
|
| 96,68
| 12,3
| 14,5
| 13,9
| |
| 97,34
| 9,8
| 14,7
| 10,1
|
| 102,68
| 10,5
| 14,7
| 12,6
| |
| 101,54
| 11,4
| 15,1
| 11,7
|
| 106,88
| 12,1
| 14,8
| 14,2
| |
| 110,35
| 10,7
| 19,8
| 9,4
|
| 115,69
| 11,4
| 9,4
| 11,9
| |
| 124,69
| 11,8
| 13,4
| 10,8
|
| 130,03
| 12,5
| 15,9
| 13,3
| |
| 119,34
| 12,7
| 16,2
| 11,5
|
| 124,68
| 13,4
| 16,2
| 14,0
| |
| 134,27
| 13,7
| 18,2
| 9,4
|
| 139,61
| 14,4
| 16,8
| 11,9
| |
| 148,94
| 14,3
| 17,5
| 12,4
|
|
| 154,28
| 15,0
| 17,5
| 14,9
| |
| 147,37
| 14,9
| 17,9
| 12,9
|
| 152,71
| 15,6
| 17,9
| 15,4
| |
| 149,28
| 14,7
| 16,3
| 15,7
|
| 154,62
| 15,4
| 18,4
| 18,2
| Табл. 7 Табл. 8
| №
| Y
| X1
| X2
| X3
|
| №
| Y
| X1
| X2
| X3
| |
| 72,59
| 10,47
| 15,64
| 11,9
|
| 77,93
| 12,77
| 19,21
| 14,4
| |
| 49,34
| 9,4
| 10,5
| 8,4
|
| 54,68
| 10,1
| 10,5
| 10,9
| |
| 52,34
| 11,4
| 11,9
| 9,1
|
| 57,68
| 12,1
| 11,9
| 11,6
| |
| 73,48
| 15,4
| 12,8
| 7,9
|
| 78,82
| 16,1
| 12,8
| 10,4
| |
| 67,34
| 12,3
| 12,4
| 8,4
|
| 72,68
|
| 12,4
| 10,9
| |
| 70,35
| 11,28
| 20,18
| 15,7
|
| 75,69
| 11,98
| 12,7
| 18,2
| |
| 80,25
| 12,49
| 15,67
| 10,4
|
|
| 85,59
| 13,19
| 14,4
| 12,9
| |
| 86,14
| 10,4
| 13,9
| 10,6
|
| 91,48
| 11,1
| 13,9
| 13,1
| |
| 91,34
| 11,6
| 14,5
| 11,4
|
| 96,68
| 12,3
| 14,5
| 13,9
| |
| 97,34
| 9,8
| 14,7
| 10,1
|
| 102,68
| 10,5
| 14,7
| 12,6
| |
| 101,54
| 17,4
| 15,1
| 11,7
|
| 106,88
| 12,1
| 14,8
| 14,2
| |
| 110,35
| 10,7
| 19,8
| 9,4
|
| 115,69
| 11,4
| 9,4
| 11,9
| |
| 124,69
| 11,8
| 15,9
| 10,8
|
| 130,03
| 12,5
| 15,9
| 13,3
| |
| 119,34
| 12,7
| 11,2
| 11,5
|
| 124,68
| 13,4
| 16,2
|
| |
| 134,27
| 13,7
| 16,8
| 9,4
|
| 139,61
| 14,4
| 16,8
| 11,9
| |
| 142,17
| 14,73
| 18,64
| 13,1
|
|
| 147,51
| 15,43
| 17,5
| 15,6
| |
| 147,37
| 14,9
| 17,9
| 12,9
|
| 152,71
| 15,6
| 17,9
| 15,4
| |
| 148,38
| 15,98
| 21,34
| 18,4
|
| 161,72
| 16,68
| 18,4
| 20,9
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|
Опухоли яичников в детском и подростковом возрасте Опухоли яичников занимают первое место в структуре опухолей половой системы у девочек и встречаются в возрасте 10 – 16 лет и в период полового созревания...
Способы тактических действий при проведении специальных операций Специальные операции проводятся с применением следующих основных тактических способов действий: охрана...
Искусство подбора персонала. Как оценить человека за час Искусство подбора персонала. Как оценить человека за час...
|
Тактические действия нарядов полиции по предупреждению и пресечению групповых нарушений общественного порядка и массовых беспорядков В целях предупреждения разрастания групповых нарушений общественного порядка (далееГНОП) в массовые беспорядки подразделения (наряды) полиции осуществляют следующие мероприятия...
Механизм действия гормонов а) Цитозольный механизм действия гормонов. По цитозольному механизму действуют гормоны 1 группы...
Алгоритм выполнения манипуляции Приемы наружного акушерского исследования. Приемы Леопольда – Левицкого. Цель...
|
|

 ,
,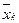 – середнє арифметичне значення вектора xk;
– середнє арифметичне значення вектора xk;  – дисперсія змінної xk.
– дисперсія змінної xk. ;
; 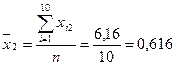 ;
;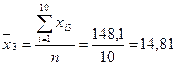 .
.

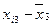





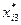
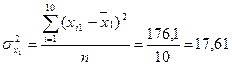 ;
;  ;
; .
. ;
; ;
; .
.
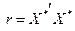 ,
, – матриця, транспонована до матриці X*.
– матриця, транспонована до матриці X*.
 ;
;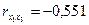 ;
;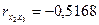 ,
, ;
; .
. =3 і рівні значущості α=0,01 критерій χ2табл.=11,34. Оскільки χ2факт <χ2табл., робимо висновок, що в масиві пояснювальних змінних не існує мультиколінеарності.
=3 і рівні значущості α=0,01 критерій χ2табл.=11,34. Оскільки χ2факт <χ2табл., робимо висновок, що в масиві пояснювальних змінних не існує мультиколінеарності. ;
; .
. ;
; ;
; .
.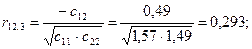
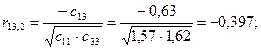
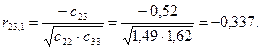
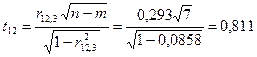 ;
; ;
;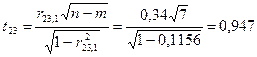 .
.


