Прогнозування за моделями простої лінійної регресії.
1. Розглянемо економетричну модель з двома змінними у загальному вигляді: y = f(x) + u, де у – залежна змінна; x – незалежна змінна; u – випадкова складова. Це проста економетрична модель. Одні і ті самі економічні процеси можна описати різними функціями, але за допомогою статистичного аналізу потрібно вибрати одну. Найпростіша форма зв’язку між двома змінними лінійна: y = a0 + a1x, де a0, a1 – невідомі параметри. Можливі й інші форми залежностей між двома змінними. Як правило нелінійні функції зводять до лінійних шляхом логарифмування або заміни: y = a0ea1x, lny = ln a0 + a1x; y = a0xa1, lny = ln a0 + a1lnx, ln x = z; y = a0 + a1/x, 1/x = z,y = a0 + a1z; y = α(1-r)x, lny = lnα + xln(1-r); y = e a0 + a1x, lny = a0 + a1x; y = 10 a0 + a1x, lgy = a0 + a1x. Нехай ми вибрали якусь із цих залежностей, визначили невідомі параметри і одержали рівняння регресії. Як відомо певна частина фактичних спостережень над змінною лежатиме вище або нижче від значень, обчислених згідно з вибраною функцією. А це свідчить про те, що вибрана функція не адекватна реальному процесу взаємозв’язків у економіці. Щоб розв’язати цю задачу, до економетричної моделі вводять стохастичну (випадкову) складову, яка акумулює в собі всі відхилення фактичних спостережень змінної у від обчислених згідно з моделлю: y = a0 + a1x +u. Стохастичну складову u економетричної моделі називають похибкою (залишком, збуренням, відхиленням). У класичній лінійній економетричній моделі змінна u інтерпретується як випадкова змінна, що має розподіл з середньою величиною, яка дорівнює нулю і сталою дисперсією Ơu². Оскільки u охоплює вплив багатьох факторів, які є незалежними, то згідно з центральною граничною теоремою теорії ймовірності можна зробити висновок, що стохастична (випадкова) складова економетричної моделі розподілена за нормальним законом. Щоб оцінити параметри моделі, потрібно сформувати сукупність спостережень, кожна одиниця якої характеризується відповідними значеннями (х;у). 2.Нехай побудували кореляційне поле точок (х;у), через які можна провести безліч прямих ліній y = a0 + a1x (рис. 1).
· · · · · · · · ·
.· · · · · · ·· ·· · · ···
· · · · · ·
0х Рис. 1.Кореляційне поле точок
Вони різняться між собою параметрами a0 і a1. Треба вибрати ту лінію, для якої б відхилення фактичних у від розрахункових ŷ було б найменшим. Принцип найменших квадратів відхилень полягає в знаходженні таких â0 і â1, для якої Σui² була б найменшою (ŷ= â0 + â1х −для розрахункових). S = Σui² = Σ (yi - ŷi) ² = Σ (yi - â0 - â1хi)² → min.
Є ще інший альтернативний спосіб обчислення параметрів â0 і â1 :
â1 = де â0 знаходиться з рівняння:
За нашим прикладом Приклад. Побудувати економетричну модель залежності витрат ресурсів на одиницю продукції (у) від рівня фондомісткості продукції (х) (дані в умовних одиницях). Розрахунки проводимо в табл.1.
Запишемо систему нормальних рівнянь:
nâ0 + â1∑хi =Σ yi; 10â0 + â11008 = 542;
â0 ∑хi + â1∑хi ²= Σ yi xi; 1008â0 + â1104784= 56221;
â0 =
â1= Економетрична модель має вигляд (для фактичних значень незалежної змінної) Y = 3,8 + 0,5 x + u.
Скориставшись альтернативним способом обчислення за допомогою відхилень середніх арифметичних, одержимо:
â1 =
де â0 знаходиться з рівняння:
1. Вихідні і розрахункові дані для побудови економетричної моделі
Оскільки вільний член моделі â0 ≠ 0 то рівень витрат на одиницю продукції не є строго пропорційним до рівня фондомісткості, â1 = 0,5 показує, що граничне збільшення витрат при зростанні фондомісткості продукції на 1 ум. од. становить 0,5 ум. од. Еластичність витрат щодо фондомісткості продукції визначається коефіцієнтом еластичності: Е = Е = 0,5 · 1,8519 = 0,93. Значення цього коефіцієнта слід тлумачити так: при збільшенні фондомісткості продукції на 1 % витрати на одиницю продукції зростуть на 0,93 %. Залишки обчислюються згідно з рівністю: ui = yi – ŷi. Оцінка дисперсії залишків подається так:
Для залишків ui можна задати певну функцію закону розподілу, наприклад функцію нормального розподілу. 3.Оцінкою коефіцієнта кореляції є вибірковий коефіцієнт кореляції, який можна обчислити за формулою:
r =
r = Вибірковий коефіцієнт кореляції є точковою оцінкою коефіцієнта кореляції і тому потребує перевірки. Вона базується на критерії Стьюдента за формулою: t= де r −вибірковий коефіцієнт кореляції; n-m− число ступенів вільності. Якщо t › tтабл. α, де tтабл. α − відповідне табличне значення t розподілу з (n –m) ступенями вільності, то можна зробити висновок про значущість коефіцієнта кореляції між залежною і незалежною змінними моделі. Для нашого прикладу: t= 4.Для аналізу якості опису існуючої залежності між двома ознаками часто використовують індекс кореляції. Він розраховується за формулою:
5. Економетрична модель – це функція чи система функцій, що описує кореляційно-регресійний зв’язок між економічними показниками, один чи кілька з них є залежною змінною, інші – незалежні. Незалежні змінні моделі називаються пояснюючими, наперед заданими змінними. Залежні змінні називаються пояснюваними змінними. Побудова будь-якої економетричної моделі здійснюється як послідовність певних кроків. Крок 1. Знайомство з економічною теорією, висунення гіпотези взаємозв’язку. Чітка постановка задачі. Крок 2. Специфікація моделі. Специфікація моделі – це аналітична форма економетричної моделі. На основі досліджуваних чинників вона складається з певного виду функції чи функцій, що використовуються для побудови моделей, має імовірнісні характеристики, які притаманні стохастичним залишкам моделі. Крок 3. Формування масивів вхідної інформації згідно з метою та завданнями дослідження. Крок 4. Оцінка параметрів економетричної моделі методом найменших квадратів. Аналіз залишків дає змогу перевірити чи не суперечить специфікація моделі передумовам “класичної” лінійної регресії. Крок 5. Якщо деякі передумови моделі не виконуються, то для продовження аналізу треба замінити специфікацію або застосувати інші методи оцінювання параметрів. Крок 6. Проведення аналізу достовірності моделі та прогнозу за побудованою моделлю. Схематично всі кроки можна зобразити так (рис. 1).
Рис.1. Етапи побудови моделі Економетрична модель базується на єдності двох аспектів – теоретичного, якісного аналізу взаємозв'язків та емпіричної інформації. Теоретична інформація знаходить своє відображення в специфікації моделі. Специфікація моделі – це аналітична форма економетричної моделі На основі досліджуваних чинників вона складається з певного виду функції чи функцій, що використовуються для побудови моделей, має ймовірнісні характеристики, які притаманні стохастичним залишкам моделі. Лінійні функції найпоширеніші в економетричному моделюванні, тому обґрунтування економетричних методів розглянемо на базі лінійних моделей. Вибір аналітичної форми економетричної моделі не може розглядатися без конкретного переліку незалежних змінних, тому специфікація моделі передбачає відбір чинників для економетричного дослідження. При цьому в процесі такого дослідження можна кілька разів повертатись до етапу специфікації моделі, уточнюючи перелік незалежних змінних та вид функції, що застосовується. Адже, коли вид функції та її складові не відповідають реальним процесам, то йдеться про помилки специфікації. Нехай економетрична модель у матричній формі має вигляд Y = XA + u, де Y – вектор значень залежної змінної; X – матриця незалежних змінних розміром n×m (n – число спостережень; m – кількість незалежних змінних); A – вектор параметрів моделі; u – вектор залишків. Залишки моделі обчислюють як різниці між фактичними значеннями залежної змінної та обчисленними за моделлю. Розглянемо передумови використання методу найменших квадратів: 1) математичне сподівання залишків дорівнює нулю, тобто M(u) = 0; 2) значення uі вектора залишків u незалежні між собою і мають постійну дисперсію, тобто M(uú)= де E – одинична матриця; 3) незалежні змінні не пов’язані із залишками: M(x́u)=0; 4) незалежні змінні моделі утворюють лінійно незалежну систему векторів, або іншими словами незалежні змінні не повинні бути мультиколінеарними.
6. Перевірку гіпотези про значущість параметрів економетричної моделі можна виконати згідно з t- критерієм: tj= Обчислене значення t- критерію порівнюється з табличним для вибраного рівня довіри і n-m ступенів вільності. Якщо tфакт> tтабл, то відповідний параметр економетричної моделі є достовірним. Дисперсії параметрів економетричної моделі можна визначити за формулами:
Отже, перевіримо гіпотези про значущість оцінок параметрів моделі побудованої на основі вихідних даних, наведених у табл.. 1 t1= t0= Якщо ступінь вільності n-m =10-2=8 і рівень значущості α=0,05 tтабл=2,306. Оскільки t1факт> tтабл , то параметр â1є значущим, t0факт < tтабл, то параметр â0 є незначущим. 7.Для подальшого аналізу побудованої економетричної моделі визначимо коефіцієнт детермінації. Він показує на скільки відсотків варіація залежної змінної визначається варіацією незалежної змінної. Перевірити на значущість коефіцієнт детермінації можна за допомогою F-критерію: Fk-1,n-k= Фактичне значення F-критерію порівнюється з табличним при ступенях вільності k-1 і n-k і при вибраному рівні значущості. Якщо Fфакт > Fтабл, то гіпотеза про значущість коефіцієнта детермінації підтверджується, у противному разі – відкидається. У нашому випадку: Fk-1,n-k= Табличне значення F-критерію при ступенях вільності 1 і 8 і рівні значущості 0,95 (F1,8(0,95)) дорівнює 5,32. Оскільки Fфакт >Fтабл, то можна зробити висновок про значущість коефіцієнта детермінації. Перевірити модель на адекватність можна за допомогою також F-критерію: Fk-1,n-k=
За даними табл. 1 фактичне значення критерію Фішера буде дорівнювати: F1,8= Оскільки Fфакт >Fтабл, можна зробити висновок, що побудована модель адекватна реальній дійсності. 8.Одним із важливих завдань економетричного моделювання є оцінка прогнозного значення залежної змінної за умови, що пояснювальна змінна задана на перспективу. На основі побудованої економетричної моделі можна отримати точковий прогноз залежної змінної на перспективу. Нехай xпрогн=130, тоді yпрогн=3,8 + 0,5 xпрогн= 3,8 + 0,5 Контрольні запитання 1. Дайте тлумачення випадкової складової економетричної моделі. 2. Які методи застосовуються для оцінювання параметрів класичної регресійної моделі? 3. У чому сутність методу найменших квадратів (1МНК)? 4. Запишіть альтернативні варіанти оцінювання параметрів моделі методом 1МНК. 5. Як можна інтерпретувати параметри простої економетричної 6. Визначіть дисперсію залишків економетричної моделі. 7. запишіть співвідношення між коефіцієнтами кореляції і детермінації. 8. Як визначаються дисперсія залишків, загальна дисперсія і дисперсія регресії? Який між ними зв’язок? 9. Як визначається F -критерій? Для чого він застосовується? 10. Покажіть залежність між F -критерієм і 11. Як оцінити достовірність коефіцієнта кореляції? 12. Як обчислюється t -критерій? . Завдання для самостійної роботи На основі статистичних даних про прибуток (Y) фірми та інвестиції (X): 1. побудувати просту лінійну економетричну модель y = a0 + a1x1 + u (y =a0 +a1x1 – за розрахунковими даними), визначивши оцінки параметрів a0, a1, виходячи з методу найменших квадратів; 2. дати економічну інтерпретацію одержаних параметрів; зобразити графічно економетричну модель (за графічними і розрахунковими даними); 3. визначити коефіцієнт еластичності та пояснити його; 4. обчислити показники тісноти зв’язку між результативною ознакою та чинником (коефіцієнт та індекс кореляції), пояснити їх; 5. перевірити суттєвість параметрів моделі та побудувати інтервали довіри для параметрів узагальненої економетричної моделі; 6. визначити коефіцієнт детермінації та перевірити його суттєвість; 7. перевірити отриману модель на адекватність; 8. на основі побудованої економетричної моделі обчислити прогнозне значення результату для заданого прогнозного значення інвестицій: Хпр.=10,5; 9. результати обчислень оформити в таблиці. Вихідні дані в умовних одиницях для різних варіантів наведено у варіантах 1 – 6.
Варіант 1 Варіант 2 Варіант 3
Варіант 4 Варіант 5 Варіант 6
|

 у
у


 · · · · · · · · · ·
· · · · · · · · · · · · · ·.· · · · · · · ·
· · · ·.· · · · · · · · · · · ·
· · · ·


 ; nâ0 + â1∑хi =Σ yi;
; nâ0 + â1∑хi =Σ yi; : â0∑хi + â1∑хi ²= Σ yiхi;
: â0∑хi + â1∑хi ²= Σ yiхi;
 .
.
 ), тобто
), тобто  = â0 + â1
= â0 + â1  .
.
 - â1
- â1  .
.
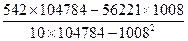 =
= 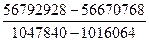 =
=  =3,84;
=3,84; =
=  =
=  =0,4993≈0,5.
=0,4993≈0,5. =
=  =0,4702≈0,5,
=0,4702≈0,5, - â1 х = 54,2 – 50,4 = 3,8.
- â1 х = 54,2 – 50,4 = 3,8. хі - х
хі - х
 (хі – х)
(хі – х)


 /
/  ;
; =
= 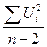 =
=  =3,325.
=3,325.
 ,
, =
=  ;
;  = 17,8258;
= 17,8258; =
=  ;
;  =9,0532;
=9,0532; =0,98.
=0,98. ,
, =
=  =13,9291.Табличне значення t − критерія для рівня значущості α =0,05 і n−m=8 ступенів вільності дорівнює 2,306. Оскільки t › tтабл. α робимо висновок, що коефіцієнт кореляції є значущим і зв’язок між x та y існує.
=13,9291.Табличне значення t − критерія для рівня значущості α =0,05 і n−m=8 ступенів вільності дорівнює 2,306. Оскільки t › tтабл. α робимо висновок, що коефіцієнт кореляції є значущим і зв’язок між x та y існує. =
=  =0,9845≈0,98.
=0,9845≈0,98.
 E,
E,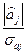 .
. =
= 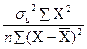 =
=  =117,62,
=117,62,  = 10,85;
= 10,85; =
= 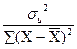 =
= 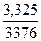 = 000098,
= 000098,  = 0,031.
= 0,031. =
=  =16,13;
=16,13; =
=  =0,35.
=0,35. :
:  .
. :
:  =194,02.
=194,02. .
. = 238,9.
= 238,9.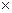 130=68,8.
130=68,8.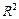 .
.


